A New Method to Solve Transportation Problem - Harmonic Mean Approach - Juniper Publishers

Juniper Publishers - Open Access Journal of Engineering Technology

Abstract

Transportation Problem is one of the models in the Linear Programming problem. The objective of this paper is to transport the item from the origin to the destination such that the transport cost should be minimized, and we should minimize the time of transportation. To achieve this, a new approach using harmonic mean is proposed in this model.

Keywords: Transportation; Harmonic mean;Optimum solution

Introduction

Transportation problem was first studied by F.L. Hithcock[1]. In transportation problem, different sourcessupply to different destinations of demand in such a way that the transportation cost should be minimized. We can obtain basic feasible solution by three methods. They are

1. North West Corner method
2. Least Cost method
3. Vogel’s Approximation method (VAM)

In these three methods, VAM method is best according to the literature. We check the optimality of the transportation problem by MODI method.

The transportation problem is classified into two types. They are balanced transportation problem and unbalanced transportation problem. If the number of sources is equal to number of demands, then it is called balanced transportation problem. If not, it is called unbalanced transportation problem. If the source of item is greater than the demand, then we should add dummy column to make the problem as balanced one. If the demand is greater than the source, then we should add the dummy row to convert the given unbalanced problem to balanced transportation problem.

In recent years, many methods are proposed to find the optimum solution for the transportation problem. Pandian &Natarajan [2] gave a new approach for solving transportation problem with mixed constraints. Korukoglu & Balli [3] discussed an improved Vogel’s Approximation method for the transportation problem. Quddos et al. [4]and Sudhakar et al. [5]developed a new method for finding an optimal solution for transportation problems. Reena et al. [6]gave the new global approach to transportation problem. Later Reena et al. [7]extended their model and gave an innovative approach to optimum solution of transportation problem. Amaravathy et al. [8]developed MDMA Method to give an optimal solution for transportation problem. Urashikumari et al. [9]investigated the new transportation problem using stepping stone method and its application. Abdul Kalam Azad et al. [10]gave an algorithmic approach to solve transportation problem with the average total opportunity cost method. Joshua et al. [11]developed a North- East Corner Method to give an initial basic feasible solution for transportation problem.

It is difficult to give the new model which fit into the real-world problems. In this paper, a new statistical method called harmonic mean is used to find the optimum solution.This method gives the solution exactly like MODI- Method and results very closer to VAM Method. We also gave the numerical example for the new method and we compared our method with existing methods such as North West Corner method, Least cost method, Vogel’s Approximation method. We checked the optimality of the solution using MODI Method. Here, we considered the balanced transportation problem also.

Harmonic mean = total number of observations/sums of the reciprocal of number.

Algorithm

1. Step 1: Check whether the given transportation problem is balanced or not. If not, balance or by adding dummy row or column. Then go to the next step.
2. Step 2: Find the harmonic mean for each row and each column. Then find the maximum value among that.
3. Step 3: Allocate the minimum supply or demand at the place of minimum value of the related row or column.
4. Step 4: Repeat the step 2 and 3 until all the demands are satisfied and all the supplies are exhausted.
5. Step 5: Total minimum cost = sum of the product of the cost and its corresponding allocated values of supply or demand.

Numerical Example

Table 1,2

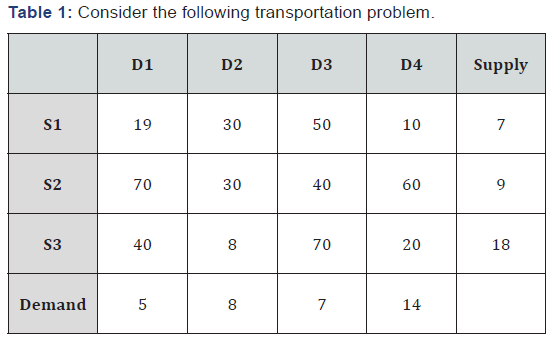
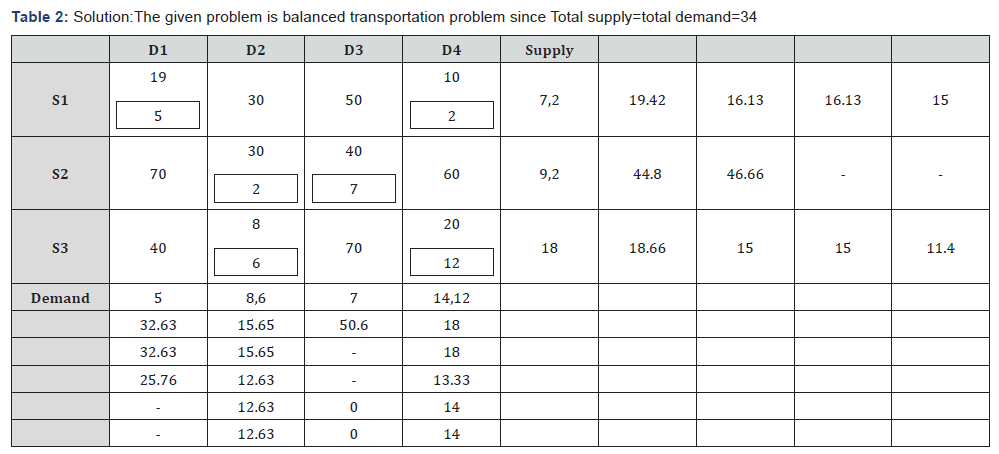
The transportation cost is:

Table3&4

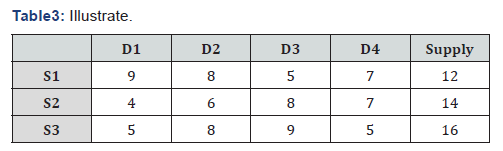
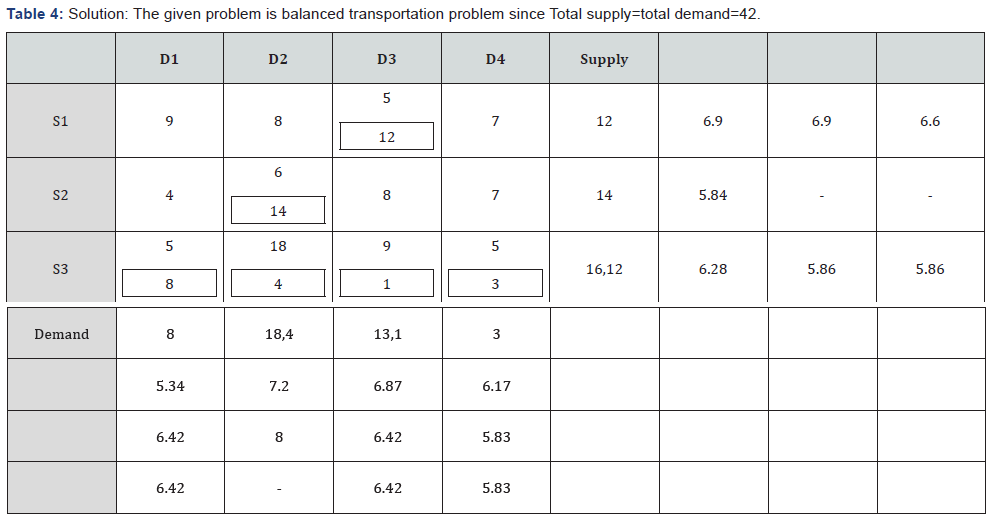
The transportation cost is:

Comparison of numerical results

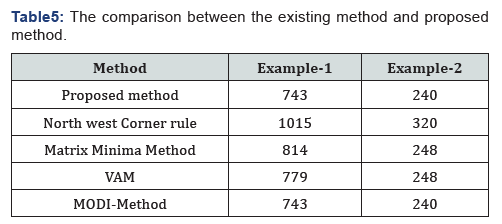
The comparison between the existing method and proposed method results are given below in Table5.

Conclusion

From the comparison table, we can observe that the optimum solution obtained by the proposed method is less than that of other methods and same that of MODI Method. But, the proposed method is very easy since we have less computation works. So, we can conclude that if we use harmonic mean approach to solve transportation problem, we can get global optimum solution in a lesser step.

For more Open Access Journals in Juniper Publishers please click on: https://juniperpublishers.com

For more articles in Open Access Journal of Engineering Technology please click on:

https://juniperpublishers.com/etoaj/index.php

For more Open Access Journals please click on: 

https://juniperpublishers.com