Administering Saturated Signalized Networks Through Fuzzy Technique-Juniper Publishers
Juniper Publishers-Open Access Journals in Engineering Technology
Abstract
An adaptive control system is developed using a fuzzy
method to improve the traffic control system performance and to reduce
the overall delay for four phases simple intersections within a grid of
network. The main functions of the developed control system are to
accelerate the cycle time and to reduce the loss time by determining the
green time for each phase based on traffic flow. The fuzzy rules are
employed using visual basic and computer-based program (Excel) to run
the validation process. The developed control system is tested on five
intersections in a simulated network in the State of Kuwait during four
different peak periods. The results indicated that the number of
vehicles passing through intersection phases has increased in most
phases by an average of 12.9%, 23.3%, 10.4% and by 21.2%. The green time
is increased by an average of 9.1%, 5.8%, 9.9% and 6.3%. Number of
intersections’ cycles remain constant at most of the time which means
that the developed control system distributes the green phases’ times
based on the traffic situation. The developed control system can be
applied on simple intersections with four perpendicular phases that
consist of collector, major arterial or minor arterial roads.
Introduction
Rapid growth of personal vehicles resulted in
excessive congestion. Traffic congestion affects operational management
of business, energy consumption and tourism. As known to the experts’
congestion reduces human productivity and leads to delays in products
and services in small and big cities. A traffic signal is among the most
important traffic control devices that are used to manage traffic flow
efficiently, but it may lead to traffic congestion if it is poorly
handled. Most traffic signals are operated by either fixed time signal
or actuated control systems. Controlling isolated traffic signal is easy
specially when the intersection demand is below the capacity, but it is
difficult when the intersection is within a network. Fuzzy techniques
are used to solve traffic problems. It might improve road capacity,
improve traffic light performance and reduce vehicle delay by adjusting
parameters such as cycle time, splits, phase sequences and offsets per
change of the traffic volume.
Fuzzy Logic Traffic Control System
The artificial intelligent concept combines the
objective knowledge, formula and equations, subjective knowledge, and
linguistic information, to assist solving traffic problems. Fuzzy is one
of the most famous artificial traffic control systems
that is used to improve the traffic situation and to increase the
traffic capacity. The fuzzy technique is used to develop the traffic
control system due to its ability to process various data, vague and
uncertain inputs of the system, and provide results that are suitable
for the decision making. Fuzzy logic is capable to incorporate human
knowledge and experience to respond quickly in unknown environments,
adapt conditions, and an ability to involve decisions with incomplete
information, complex equations, and non-linear processes. It allows the
manipulation of linguistic inexact data as a useful tool in the design
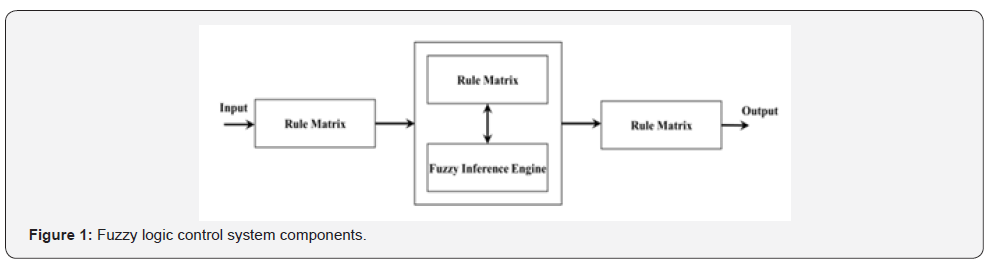
of the intelligent traffic control system. The fuzzy logic control
system consists of different components: fuzzification, fuzzy control
decisions block; rule matrix and fuzzy interference engine; and
defuzzification as shown in Figure 1.
Based on a literature survey of the application of
fuzzy control traffic systems, it can be observed that the
implementation of fuzzy systems in transportation has a large impact on
traffic levels. Consequently, the following highlights can be made:
Traffic fuzzy systems had different shapes, which are often recurrent;
improving flow rate, forecasting traffic capacity, controlling phase
selection, and controlling signal timing. Most of the researchers used
Mamdani type inference and depended on historical data to compare
between the proposed and existing
systems. Many researchers work on control of an isolated
intersection with fuzzy control method [1-5]. Few of them work
in a simple isolated intersection [6,7]. A few of them work in a
roundabout intersection [8,9]. Furthermore, some researchers
work on T-intersection [10,3,11]. Many others worked on twoway
intersections [3,12,13]. Few researchers apply a fuzzy logic
system to the coordinated control of arterial or area traffic.
Finally, the results showed that the traffic performance of Fuzzy
Logic Traffic Control Systems has better performance than
traditional traffic signal controls, specifically during heavy and
uneven traffic volume conditions.
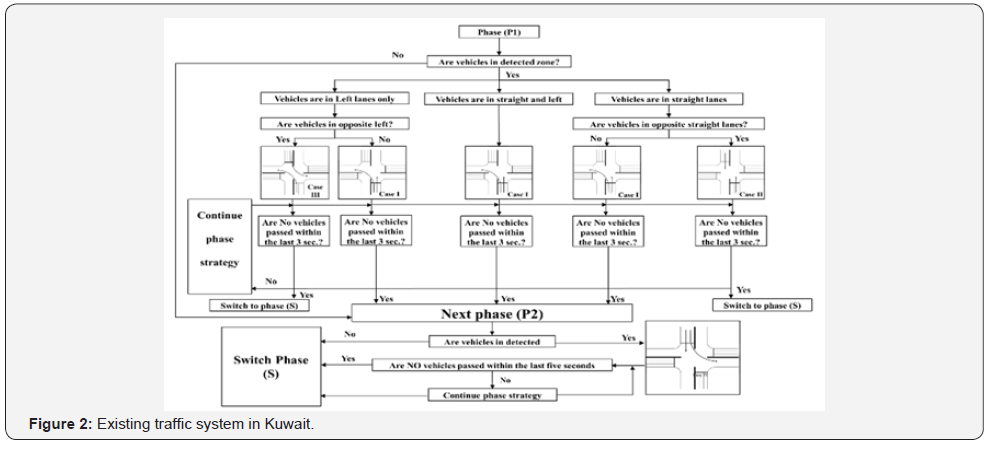
Existing Traffic Control System in Kuwait
The signal control system strategies used in the State of
Kuwait to control the flow and vehicle movements are either
fixed time or semi-actuated signal control systems. The fixed
time control system is used in all the intersections through the
day in non-peak periods. Whereas, the semi-actuated control
system is used only for the free time periods to adjust the
green phases time continuously. The order and the sequence of
the phases are fixed during the fixed time control system. The
traffic signal timing plans are generated in Kuwait by a Synchro
program, where each intersection has its timing and phasing
strategy. The block diagram for the existing system in Kuwait is
shown in Figure 2.
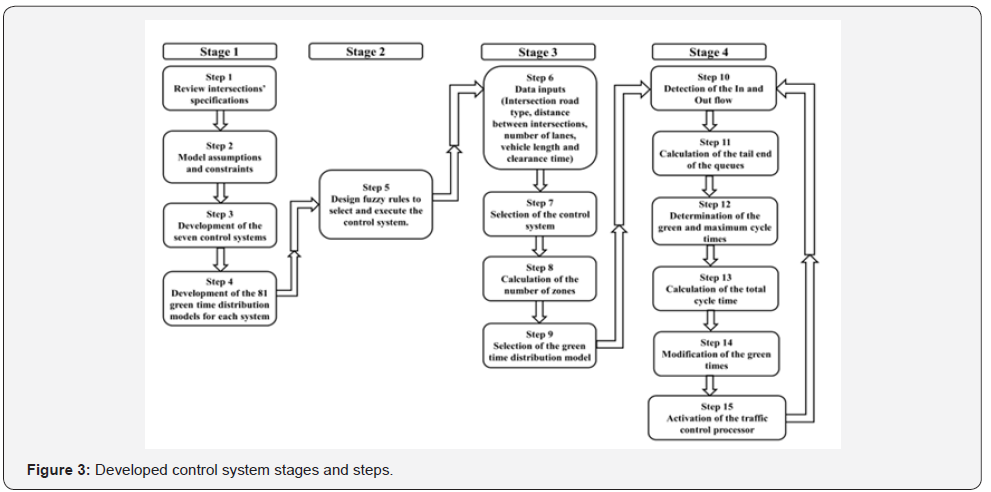
Proposed System
The developed control system is designed based on the
principle being that the vehicle can move ahead only if there is
a space for passing. The developed control system is designed
using a fuzzy expert system that is different from the traditional
control system methods. Detectors are placed at every entry
and exit of the intersections to count the number of cars passing
through the intersection. The developed control system is
designed through four stages where each stage is designed
through several steps. Each stage has different inputs and
outputs and a different function. Figure 3 shows the design
stages and the steps of each stage. Stage 1: design of the green
time distribution models through steps 1 to 4, Stage 2: design of
the fuzzy rules for the selection of signal timings through step 5,
Stage 3: initialization of the control system through steps 6 to 9,
and Stage 4: execution of the developed control system through
steps 10 to 15.
Stage 1: Design of the Green Time Distribution Models
Stage 1 is realized through step 1 to step 4. At step 1, the
intersections’ specifications, geometries, road types, vehicle
movement strategies, traffic devices, control systems in addition
to the fuzzy control systems are reviewed, analyzed and compared
to develop the control system constraints and assumptions.
At step 2, a list of system assumptions and constraints were
specified as follow: the control system is designed for an
unsynchronized simple intersection with four perpendicular
phases. Each phase consists of three vehicle movements as
straight-through, left, and right turns. The control system is
designed for all traffic conditions (under saturation, saturation,
and over saturation). The system is developed based on the flow
that arrives and departs in a deterministic, uniform and steady
way and distributed equally on the phases lanes. The distance
between the intersections (Ld ) , ranged between (Ld )max = 2400m
and ( ) 800 d L min = m. The distance length between two intersections
is divided into several zones (Z). The minimum distance length
unit zone ( ) 800 unit Z = m , and the last zone of the intersection phase
is critical zone ( ) critical Z . The vehicle length to be used in system
calculation is specified as a medium personal vehicle with length
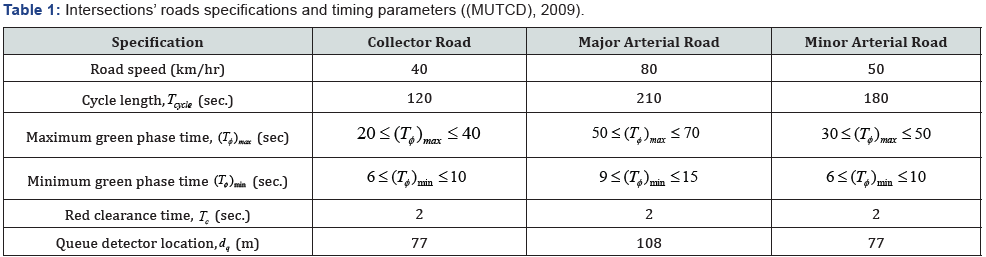
( ) 7.5 lV = m . The timing parameters (cycle time, maximum and
minimum phase green time, red clearance time and the queue
detector location) for each road type and speed are specified as
shown in Table 1.
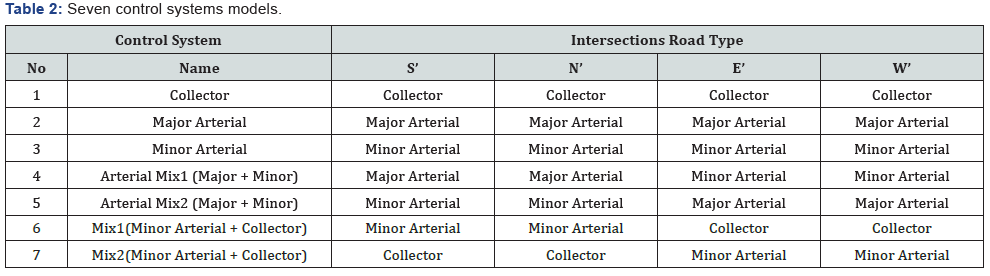
At step 3, seven control systems are developed for a
combination of intersection of two road types (collector, major
arterial, and minor arterial) as shown in Table 2. The control
systems are named by the intersection roads type.
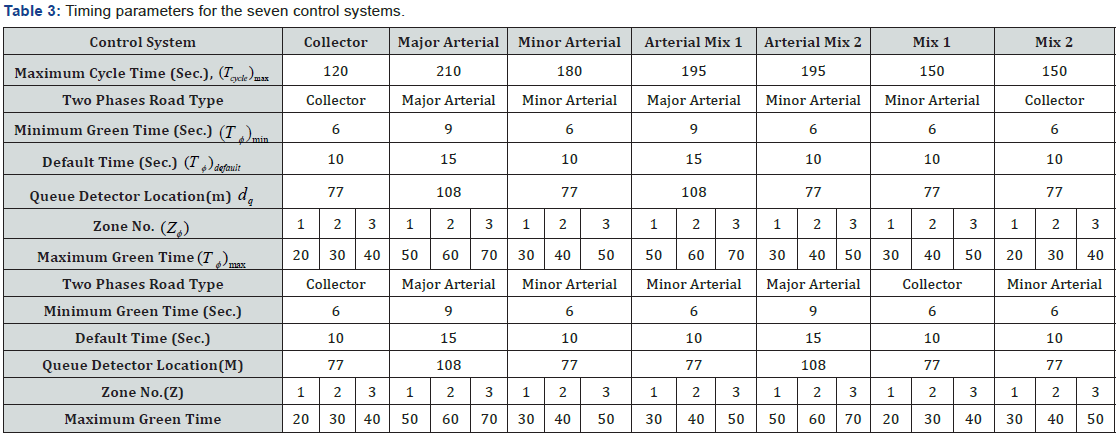
For each control system, a scenario of eighty-one green time
distribution models are developed and tabled at step 4. These
tables are filled with the timing parameters (maximum cycle
time, minimum green time, default time and maximum green
time) that are specified based on the system designing rules as
shown in Table 3.
Timing parameters are specified for a specific number of zones,
but for better accuracy, each zone is divided into intervals
where each interval 0.5* 400 unit = Z = m except the first and second
intervals. The first interval is specified by the distance between
stop-line and queue detector location ( ) q d , and the second
interval is specified by the distance between queue detector
location and 400 m away from queue detector. The green time
for each interval is calculated as the ratio between the interval
length and the whole length as in Eqn (1).

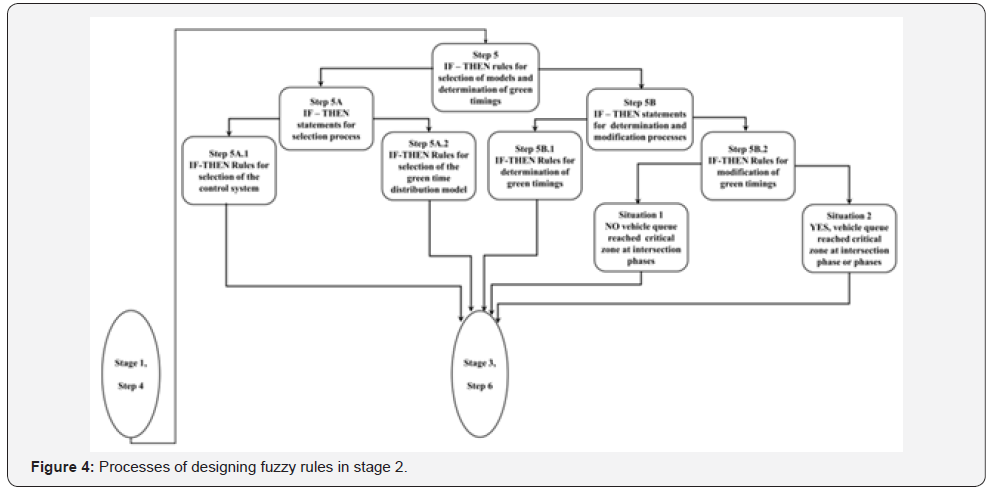
Stage 2: Design of Fuzzy Rules for Signal Timings
At step 5 sets of fuzzy rules are designed to determine the
signal timing through two processes. The first process is to select
the actual green time distribution model. The second process is
to determine the intersection timing parameters. The fuzzy rules
for the selection process are designed in step 5A which is divided
into 5A.1 and 5A.2. The fuzzy rules for execution process of the
developed control system are designed in step 5B, which in turn
is divided into 5B.1 and 5B.2 as shown in Figure 4.
Stage 3: Initialization of the Control System
Stage 3 is designed through steps 6 to 9 for initialization
of the control system. Several inputs are specified in step 6.
These are to be used in different steps based on their calls and
functions in the selection and actual run processes. These inputs
are: the intersection in terms of road types (used for selection
the control system model); distance between intersections ( ) d L
(used for selection the green time distribution model); number
of lanes (n ) φ ; vehicle length ( ) Vl (used for running process); and
clearance time (Tc) (used for modification process). At step 7,
the system processes the intersection roads’ types (input) by the
first set of the fuzzy rules 5A.1, (Figure 4) to select the actual
control system from the seven developed control systems. At
step 8, the system retrieves the distance Ld) and calculates
the number of zones at each intersection phase. At step 9, the
system processes the calculated number of zones by the second
set of fuzzy rules 5A.2, (Figure 4) to select the actual green time
distribution model from the eighty-one models.
Stage 4: Execution of the Developed Control System
Stage 4 is designed through steps 10 to 15 for execution of
the developed control system. Running the developed control
system depends on the system inputs, fuzzy rules, and the
flow in/out that is read by the system detectors. At step 10, the
developed control system reads the traffic flow entering the
intersection from the four directions by gridlock detectors that
are placed at the entrance of the phases. At the same time, the
control system reads the traffic flow exiting from the intersection
to the surrounding four directions by step-line detectors that
are placed at the stop-line. The system at step 11 calculates the
vehicle residual using Eqn (2).
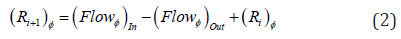
Where; Ri+1) φ is number of residual vehicles formed in the
(cycle) i+1 , (Flowφ)out , number of vehicles entering the intersection
phase during the cycle time, (Flowϕ)Out, number of vehicles
exiting from the intersection phase during the green phase time,
(Ri) φ , number of the residual vehicles from the (cycle) i+1 . After
calculating the vehicle residual, the system calculates the queue
length in each phase of the intersection as follow:

Where: Zφq is the queue length at the intersection phase
in meter, nφ , number of lanes for the considered intersection
phase, Vl , average vehicle length in meter.
At step 12, the control system processes the calculated
vehicle queue to determine the green times (Tφ) , clearance
time (Tc) , and the maximum cycle time (Tcycle)max from green time
distribution model by applying the fuzzy rules (5B.1, (Figure 4).
The control system at step 13 calculates the total cycle time ( )total T
as follows:
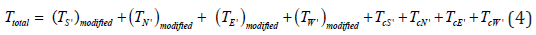
Where; φ is the intersection phase, Tφ , the phase green
time in the green time distribution models in second, Tc , the
clearance time in second.
During the clearance time of the last phase, the system
modifies the determined green time.
The modification process is an important process in the
control system that happens during the clearance time of the
last phase. The system at step 14 processes the vehicle queues
and their locations in the intersection phases with the relation
between (T)cycle and (T)total by applying the fuzzy rules (5B.2,
(Figure 4) to modify and change the control system green phases
times. At step 15, the control system sends to the traffic signal
the actions for the next cycle timing. At step 16, the control
system provides a report that includes intersection cycle time,
green times, phases flow in (flow)In , phases flow out (flow)Out and
vehicle queue length to be used in the system analysis.
Results
Real life test for the validity test of the control system was
not possible due to the cost constraint and excessive time
needed to acquire approvals from several ministries. Therefore,
historical data are used for traffic simulation of an existing grid
network controlled by the developed system. Hence, system
performance can be measured and compared with the existing
traffic control system. The developed control system is applied
to a network of thirteen intersections in Kuwait town having the
system conditions and criteria. The five central intersections
in the network are specified for running the developed control
system by using their data to measure the system performance.
The results of the individual intersections and for the network
are presented next.
Intersections’ results:
The sample network considered consists of five intersections,
where each intersection consists of four phases (total of 20 phases
in the sample network). Table 4 shows the simulated results of
the developed system compared with the existing system for
vehicle passing intersections’ phases and the time needed to
pass through these intersections during four considered periods.
The simulated results of the developed system for
periods
6:45 to 7:00 and 14:15 to 14:30 show that 55%, i.e. 11 out of
20 phases, of the network phases exhibit increases in both the
number of vehicles crossing during the green phase relative to
the performance of the existing system. Furthermore, 30% of
the network phases exhibit increases in the number of passing
vehicles, but they show decreases in the green time. That means, there
is a loss in the green time in the existing control system
and the green time is distributed in insufficient way where the
developed control system distributes the green time based on
the traffic flow. However, 10% of the network phases show
decreases in both the number of passing vehicles and the green
time. Where, the existing control system distributes extra green
time where it is not needed. Results show that 5% of the network
phases show decreases in the number of passing vehicles and
increases in the green time.
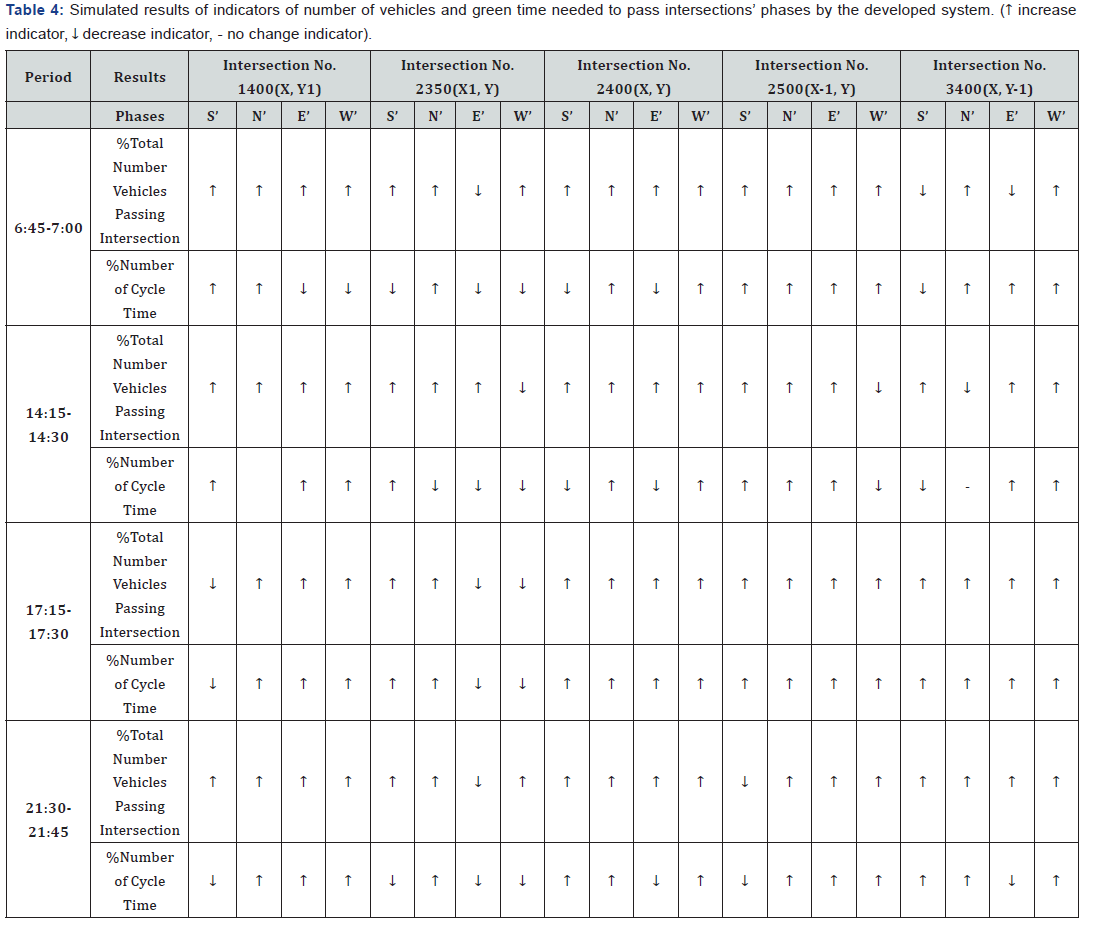
The results of the period 17:15 to 17:30 show that 85% of the
network phases exhibit increases in both the number of passing
vehicles and the green time. However, 15% of the network
phases show decreases in both the number of passing vehicles
and the green time. Furthermore, the results of the period 21:30
to 21:45 show that 65% of the network phases resulted in
increases in both the number of passing vehicles and the green
time. Whereas, 25% of the network phases show increases in the
number of passing vehicles and decreases in the green time. For
this same period, 10% of the network phases show decreases in
both the number of passing vehicles and the green time. From
previous analysis, 85%, i.e. 17 out of 20 phases, of the phases in
the network show increases in the number of vehicles passing
through phases during 6:45 to 7:00, 14:15 to 14:30, and 17:15
to 17:30 periods, while 100% of the phases in the network show
increases during the period 21:30 to 21:45.
The simulated overall results of the developed system for the
total number of vehicles passing intersections’ phases and the
number of cycles during the four specified periods are shown in
Table 5.
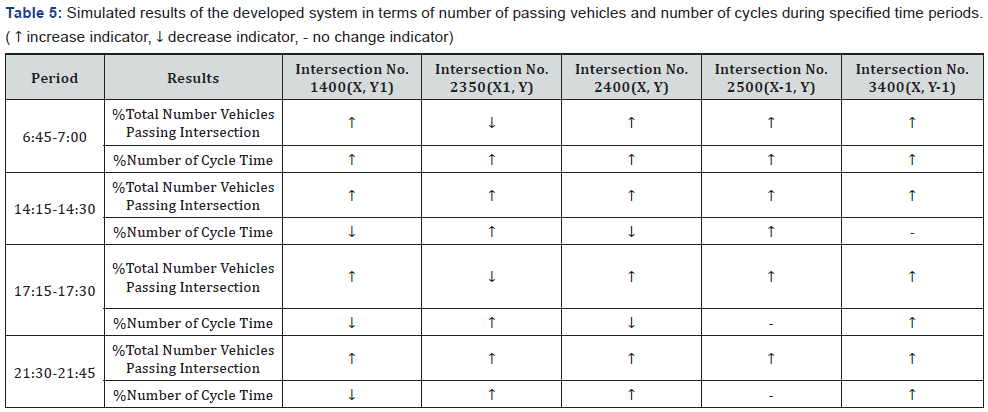
As can be observed from Table 5, 80% of the network
intersections show increases in the total number of vehicles
passing the intersections during the periods 6:45 to 7:00 and
17:15 to 17:30. On other hand, 100% of the network intersections
show increases in the total number of vehicles passing the
intersections during the periods 14:15 to 14:30 and 21:30 to
21:45. All the intersections showed higher number of cycles
during specified period during 6:45 to 7:00. That means the
developed system shortened and accelerated the cycles through
the specified periods to reduce the waiting time. Forty percent
of the intersections show increases during the periods 14:15 to
14:30 and 17:15 to 17:30, while 20% do not show changes in the
number of cycles during these periods. Furthermore, 60% of the
intersections Showed higher number of cycles during the period
21:30 to 21:45.
Table 6 presents the percentages of the differences in the
number of vehicles passing intersections’ phases between the
developed and existing systems, and the percentages of the
differences in the green times needed to pass through these
phases during the four periods (6:45 to 7:00, 14:15 to 14:30,
17:15 to 17:30, 21:30 to 21:45).
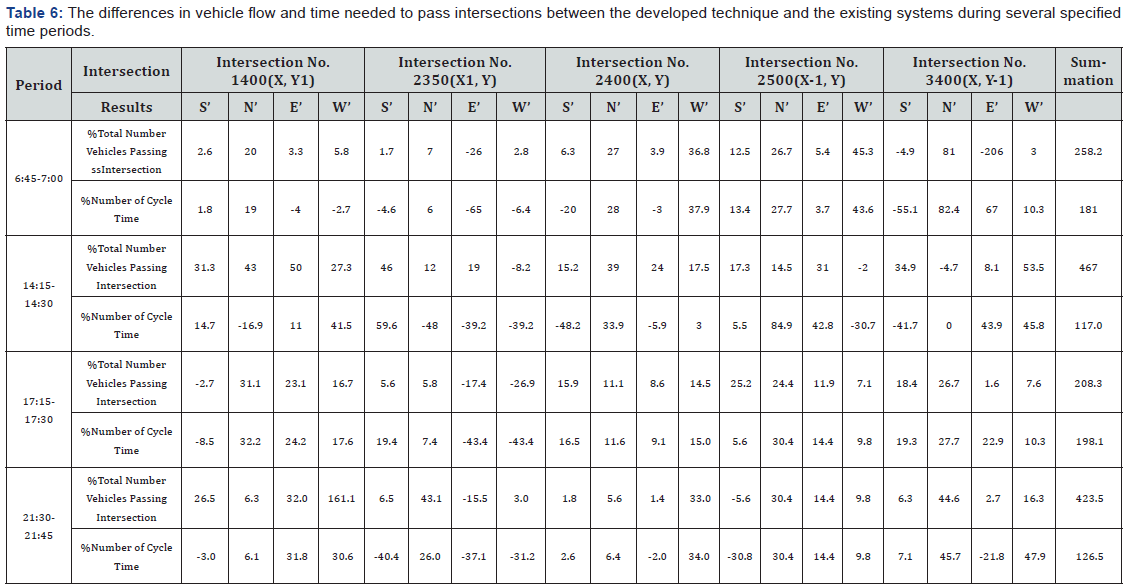

vFor period 6:45 to 7:00, the total percentages of the
differences between number of vehicles passing the five
intersections’ phases (20 phases) is increased by 258.2%. For
the five intersections, the average percentage of the number of
vehicles passing the intersections’ phases is increased by 12.91%
(258.2%/20 phases).The total percentages of the differences between
green time needed to pass through the five intersections’ phases
is increased by 9.05% (181%/20 phases). By comparing the increasing
of percentages in number of vehicles passing the intersections’
phases to the increasing of percentages in green time needed
for vehicles to pass these phases, the increase in the green time
is less than the increase of number of vehicles. This means, the
developed control system improves the network performance by
increasing number of vehicles passing the intersections’ phases
during the period 6:45 to 7:00.
For period 14:15 to 14:30, the total percentages of the
differences between number of vehicles passing the five
intersections’ phases (20 phases) is increased by 467%. For
the five intersections, whereas the average percentage of
the number of vehicles passing the intersections’ phases is
increased by 23.3% (467%/20 phases). The total percentages of the
differences between green time needed to pass through the five
intersections’ phases is increased by 5.85% (117%/20 phases).
For period 17:15 to 17:30, the total percentages of the
differences between number of vehicles passing the five
intersections’ phases (20 phases) is increased by 208.3%. For the
five intersections, while the average percentage of the number of
vehicles passing the intersections’ phases is increased by 10.4%
(208.3%/20 phases). The total percentages of the differences between green
time needed to pass through the five intersections’ phases is
increased by 9.9% (198.1%/20 phases).
Furthermore, for period 21:30 to 21:45, the total percentages
of the differences between number of vehicles passing five
intersections’ phases (20 phases) is increased by 423.5%. For
the five intersections, the average percentage of the number of
vehicles passing the intersections’ phases is increased by 21.2%
(423.5%/20 phases). The total percentages of the differences between green
time needed to pass through the five intersections’ phases is
increased by 6.3% (126.5%/20 phases)
Network results
The testing sample, as mentioned earlier, consisted of a grid
network considering four directions; S’, N’, E’ and W’, within each
direction a set of three successive intersections are considered.
The increasing and decreasing tendencies in the percentage
differences between number of vehicles passing through the
network directions between the developed technique and the
existing system, along with the necessary time for the vehicles to
pass through these directions during certain tested periods, are
shown in Table 7.
The results of period 6:45-7:00 show that the number of
vehicles passing through the S’ direction is increased and the
time to pass the vehicles through same directions is decreased,
number of vehicles and the time needed to pass through the N’
direction are increased, as well as in W’ direction, while number
of vehicles and the time needed to pass through E’ direction are
decreased as shown in Table 7. That means, 25% of the network
(direction S’) exhibits increase in the number of vehicles and
decreases in the time needed to pass through S’ direction. And,
50% of the network (directions N’ and W’) exhibits increases in
both the number of vehicles and the time needed to pass through
these directions. Whereas, 25% of the network (direction E’)
exhibits decreases in both the number of vehicles and the time
needed to pass through this direction.
The results of period 14:15-14:30 show that the number of
vehicles passing through the S’, E’ and W’ directions is increased
and the green time to pass the vehicles through same directions
is decreased. Whereas the number of vehicles passing through
the N’ direction is decreased, and the green time needed to
pass through the direction is increased. That means, 75% of
the network (directions S’, E’ and W’) exhibits increases in the
number of vehicles and decreases in the green time needed to
pass through these directions. And, the 25% of the network
(direction N’) exhibits decreased in the number of vehicles and
increase in the green time needed to pass through N’ direction.
The results of period 17:15-17:30 show that the number of
vehicles and the green time needed to pass through the S’, and N’
directions are increased. The number of vehicles passing through
E’ direction is increased while the green time needed to pass through this direction is decreased. For direction W’, the number
of vehicles and green time needed to pass through the direction
are decreased. That means, 25% of the network (direction E’)
exhibits increases in the number of vehicles passing through the
direction and decreases in the green time needed to pass through
this direction. Fifty percent of the network (directions S’ and N’)
exhibits increases in the number of vehicles and the green time
needed to pass through these directions. Furthermore, 25%
of the network (direction W’) exhibits decreases in both the
number of vehicles and the green time needed to pass through
W’ direction.
The results of the last period 21:30-21:45 show that the
number of vehicles and the green time needed to pass through
the S’, N’ and W’ directions are increased. The number of
vehicles passing through E’ direction is increased while the
green time needed to pass through this direction is decreased.
That means, 25% of the network directions represented by E’
exhibit increases in the number of vehicles passing through the
direction and decreases in the green time needed to pass through
this direction. While, the 75% of the directions (S’, N’, and W’)
exhibits increases in both the number of vehicles and the green
time needed to pass through these directions.
Conclusion
A fuzzy system is utilized to control the setting of a network
of signalized intersections. The design consisted of two stages;
a modelling system for green time distribution based on the
intersections roads geometric specifications; and designing fuzzy
rules that are implemented by using visual basic and computerbased
program (Excel). The objective of the developed control
system is to increase flow crossing the various intersection
phases in lesser than the existing technique by distributing
the green time of the intersections’ phases based on the traffic
situation.
The developed control system is applied on five intersections
in a grid of a network during four different periods during the
day. It is evaluated by simulating a real network using actual data,
and the performance results are compared with the historical
results obtained by the existing control system. The developed
control system reduces the waste in the green time of some
phases that are specified by the existing system. This time loss is
added to the other phases of the developed control system. The
developed control system increases the intersection cycle time
to its maximum to increase the green interval. That appears in
the cases where the number of passing vehicles and the green
time are increased.
Some results show that the green time is reduced by the
developed control system while the number of passing vehicles
is increased. It means that the associated phase has a time loss
exercised by the existing system. The existing system specifies
the green time as a constant at each period while the developed
control system specifies it based on the traffic situation. The
developed control system reduces the green time in some
phases since the traffic of these phases does not reach its critical
situation. This yields in decreasing the number of passing
vehicles through these phases.
For the cases where the number of vehicles passing the
phases is decreased and the green time is increased, it means
that application of the developed control system rules increases
the total cycle time to the maximum. The developed system
distributes the green time among the four phases based on the
traffic situation. Thus, when a phase has long distance and long
queue, the control system gives this phase further green time.
The developed control system increases the number of
vehicles passing through the network directions, and at the same
time increases the time, which means that the developed system
reduces the time loss from the other directions and adds it to the
critical direction. The developed control system decreases the
trip time, which means that the system eliminates the time loss
from a direction and distributes it to the other directions. For
the directions where the traffic is not in a critical situation, the
developed system decreases both the trip time and the number
of vehicles passing in these directions in the network.
The developed system increases the number of the passing
vehicles at most phases for most periods while the green time
is increased in some phases and it is decreased in other phases.
The developed system reduces the time loss from some phases
and adds it to the phase that needs it to increase the number
of vehicles passing through. Furthermore, the green time
is increased in some intersections while in others remains
constant where the system increases the total cycle time to the
maximum and adds the extra time to the phases in need. The
time is decreased in some phases by the developed system while
the passing vehicles number is increased where the developed
control system reduces the time loss from these phases.
The total cycle time in the developed control system is
specified dynamically based on the traffic situation and the
vehicle queue at the phases. Thus, the number of cycles is varying
based on the traffic situation.
The developed system can be used to control the
intersections having similar specifications that the developed
control system is built for. The intersections should be simple
with four perpendicular phases, and consist of the collector,
major arterial and minor arterial roads’ specifications. Each road
should include three detectors (stop line, queue, and gridlock)
to obtain actual traffic data. Any changes in the variables such
as clearance time, vehicle length, number of lanes, etc. should be
used as new inputs to run the system.
The green times in the green time distribution models could
be distributed in any other way for the similar control system
model’s specifications as number of zones and the probability
of combination between them. The new green time distribution
models can be used by the developed control system with the
same fuzzy rules.
For more articles in Open Access Journal of
Engineering Technology please click on:




Comments
Post a Comment