Non-Dominated Sorting Moth Flame Optimizer: A Novel Multi-Objective Optimization Algorithm for Solving - Juniper Publishers Engineering Design Problems -
Juniper Publishers - Open Access Journal of Engineering Technology
Abstract
This novel article presents the multi-objective
version of the recently proposed Moth-flame optimizer (MFO) known as
Non-Dominated Sorting Moth Flame Optimizer (NSMFO). This proposed NSMFO
algorithm works in such a manner that it first collects all
non-dominated Pareto optimal solutions achieved till the evolution of
last iteration limit. The best solutions are then chosen from the
collection of all Pareto optimal solutions using a crowding distance
mechanism based on the coverage of solutions as navigation strategy to
guide moths towards the dominated regions of multi-objective search
spaces. For validate the efficiency and effectiveness of proposed NSMFO
algorithm is applied to a set of standard unconstrained, constrained and
engineering design problems. The results are verified by comparing
NSMFO against Multi objective Colliding Bodies Optimizer (MOCBO), Multi
objective Particle Swarm Optimizer (MOPSO), non-dominated sorting
genetic algorithm II (NSGA-II) and Multi objective Symbiotic Organism
Search (MOSOS).The results of proposed NSMFO algorithm validates its
efficiency in terms of Execution Time (ET) and effectiveness in terms of
Generalized Distance (GD), Diversity Metric (DM) on standard
unconstraint, constraint and engineering design problem in terms of high
coverage and faster convergence.
Keywords: Non-dominated; Crowing distance; NSMFO algorithm; Multi-objective algorithm; Economic constrained emission dispatchAbbrevations: NSMFO: Non-Dominated Sorting Moth Flame Optimizer; MOCBO: Multi Objective Colliding Bodies Optimizer; MOPSO: Multi Objective Particle Swarm Optimizer; MOSOS: Multi Objective Symbiotic Organism Search; ET: Execution Time; GD: Generalized Distance; DM: Diversity Metric
Introduction
Optimization is a work of achieving the best result
under given limitation or constraints. Now a day, optimization is used
in all the fields like construction, manufacturing, controlling,
decision making, prediction etc. The final target is always to get
feasible solution with minimum use of resources. In this field computers
make a revolutionary impact on every field as it provides the facility
of virtual testing of all parameters that are involved in a particular
design with less involvement of human efforts, benefits in less time
consuming, human efforts and wealth as well.
Today we use computer-aided design where a designer
designs a virtual system on computer and gives only command to test all
parameters involved in that design without even the need for a single
prototype. A designer only to design and simulate a system and set all
the parameter limitation for the computer.
Computer-aided design technique becomes more
effective with the additional feature of auto-generation of solutions
after
it’s mathematically formulation of any system or design problem.
Auto generation of solution, this feature is come into nature with the
development of algorithms. In past years, real world designing problems
are solved by gradient descent optimization algorithms. In gradient
descent optimization algorithm, the solution of mathematically
formulated problem is achieved by obtaining its derivative. This
technique is suffered from local minima stagnation [1,2] more time
consuming and their solution is highly dependent on their initial
solution.
The next stage of development of optimization
algorithms is population based stochastic algorithms. These algorithms
had number of solutions at a time so embedded with a unique feature of
local minima avoidance. Later population-based algorithms are developed
to solve single objective at a time either it may be maximization or
minimization on accordance the problems objective function. Some popular
algorithms for single objective problems are Grey wolf optimizer (GWO)
[3], Bat algorithm (BA) [4], Particle swarm optimization (PSO) [5], Ant
colony optimization (ACO) [6], Genetic algorithm (GA) [7], Cuckoo search
(CS) [8], Mine blast algorithm (MBA) [9], Krill Herd (KH) [10],
Interior search
algorithm (ISA) [11] etc. These algorithms have capabilities to
handle uncertainties [12], local minima [13], misleading global
solutions, better constraints handling etc [14,15]. To overcome
these difficulties different algorithms are enabled with different
powerful operators. As mention above here is only objective then
it is easy to measure the performance in terms of speed, accuracy,
efficiency etc. with the simple operational operators.
In general, real world problems are nonlinear and multiobjective
in nature. In multi-objective problem there may be some
objectives are consisting of maximization function while some are
minimization function. So now a day, multi-objective algorithms
are in firm attention.
Let’s take an example of buying a car, so we have many
objectives in mind like speed, cost, comfort level, space for number
of people riding, average fuel consumption, pick up time required
to gain particular speed, type of fuel requirement either it is diesel
driven, petrol driven or both etc. To simply understand multiobjective
problem, from Figure 1, we consider two objectives,
first cost and second comfort level. So we go for sole objective
of minimum cost possible then we have to deny comfort level
objective and vice-versa. It means real word problems are with
conflicting objectives. So as, we are disabled to find an optimal
solution like single objective problems. About multi-objective
algorithm and its working is detailed described in next portion of
the article.

Figure1 Car-buying decision-making problem (Hypothetical
Optimal solutions). The No free launch [16] theorem that logically
proves that none of the only algorithm exists equally efficient for
all engineering problem. This is the main reason that it allows
all researcher either to propose new algorithm or improve the
existing ones. This paper proposed the multi-objective version of
the well-known moth flame optimizer (MFO) [17]. In this paper
non-sorted MFO (NSMFO) is tested on the standard un-constraint
and constraint test function along with some well-known
engineering design problem, their results are also compared
with contemporary multi-objective algorithms Multi objective
Colliding Bodies Optimizer (MOCBO) [18], Multi objective Particle
Swarm Optimizer (MOPSO) [19,20], Non-dominated Sorting
Genetic Algorithm (NSGA) [21-23], non-dominated sorting
genetic algorithm II (NSGA-II) [24] and Multi objective Symbiotic
Organism Search (MOSOS) [25] that are widely accepted due to
their ability to solve real world problem.
The structure of the paper can be given as follows: - Section
2 consists of literature; Section 3 includes the proposed novel
NSMFO algorithm; Section 4 consists of competitive results
analysis of standard test functions as well as engineering design
problem and section 5 includes real world application, finally
conclusion based on results and future scope of work is drawn.
Literature Review
As the name describes, multi-objective optimization handles
simultaneously multiple objectives. Mathematically minimize/
maximize optimization problem can be written as follows:
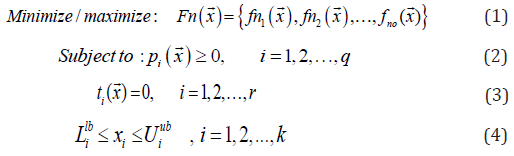
Where q is the number of inequality constraints, r is the
number of equality constraints is the number of variables, pi
is the ith inequality constraints, no is the number of objective
functions, ti indicates the ith equality constraints, and [Lil,Uiub]are
the boundaries of ith variable.
Obviously, relational operators are ineffective in comparing
solutions with respect to multiple objectives. The most common
operator in the literate is Pareto optimal dominances, which is
defined as follows for minimization problems:
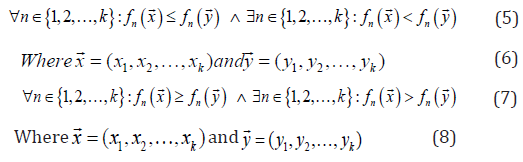
These equations show that a solution is better than another
in a multi-objective search space if it is equal in all objectives and
better in at least one of the objectives. Pareto optimal dominance
is denoted with ≺ and ≻. With these two operators’s solutions can
be easily compared and differentiated.
Population based multi-objective algorithm’s solution
consists of multiple solutions. But with multi-objective algorithm
we cannot exactly determine the optimal solution because each
solution is bounded by other objectives or we can say there is
always conflict between other objectives. So the main function
of stochastic/population based multi-objective algorithm is to
find out best trade-offs between the objectives, so called Pareto
optimally set [26-28].
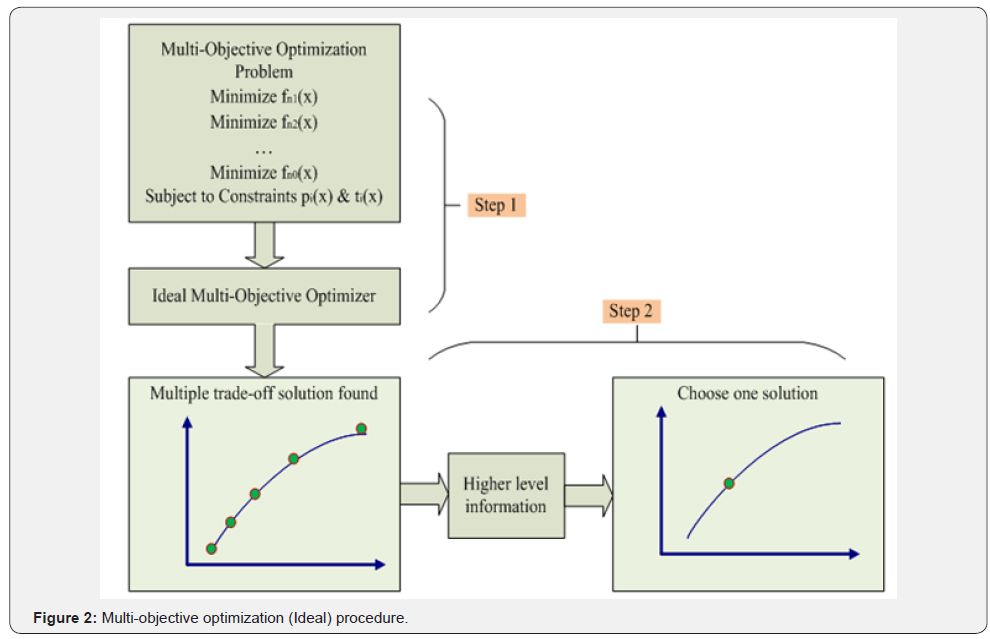
The principle of working for an ideal multi-objective
optimization algorithm is as shown in Figure2.
Step No. -1 Find maximum number of non-dominated solution
according to objective, it expresses the number of Pareto
optimal set so as shows higher coverage
Step No. -2 Choose one of the Pareto optimal solution using
crowding distance mechanism that fulfils the objectives.
Now a days, recently proposed sole objective algorithms are
equipped with powerful operators to provide them a capability
to solve multi-objective problems as well. In the same manner we
proposed NSMFO in a hope that it will perform efficiently for multiobjective
problems. These are: Multi-objective GWO [29], Multiobjective
Bat Algorithm [30], Multi-objective Bee Algorithm [31],
Pareto Archived Evolution Strategy (PAES) [32], Pareto-frontier
Differential Evolution (PDE) [33], Multi-Objective Evolutionary
Algorithm based on Decomposition (MOEA/D) [34], Strength-
Pareto Evolutionary Algorithm (SPEA) [35,36] and Multi-objective
water cycle algorithm with unconstraint and constraint standard
test functions [37,38].Performance measurement for approximate
robustness to Pareto front of multi-objective optimization
algorithms in terms of coverage, convergence and success metrics.
The computational complexity of NSMFO is order of O(mn2 )
where N is the number of individuals in the population and M is the
number of objectives. The complexity for other good algorithms in
this field: NSGA-II, MOPSO, SPEA2 and PAES areO(mn2 ) . However,
the computational complexity is much better than some of the
algorithms such as NSGA and SPEA which are ofO(mn3 ) .
Non-Dominated Sorting Moth Flame Optimizer (NSMFO)
Moth-flame optimizer (MFO) algorithm with sole objective
was proposed by Mirjalili Seyedali in 2015 [17]. It is basically a
stochastic population based, nature inspired algorithm. In this
algorithm the basic strategy of navigation for travelling long
distances in straight direction having a constant angle w.r.t moon
(flame) is utilized by insects (Moths) in night. However, this
strategy efficiently works only for the targeted flame is far distance
away from the moths but fails if flame is nearer. Generally, if flame
is far from moth then it is easy for the moths to keep the constant
angle from it, but in opposite case when flame is nearer then the
angle continuously decreasing and finally moths tends to dip into
flame (targeted optimal solution).
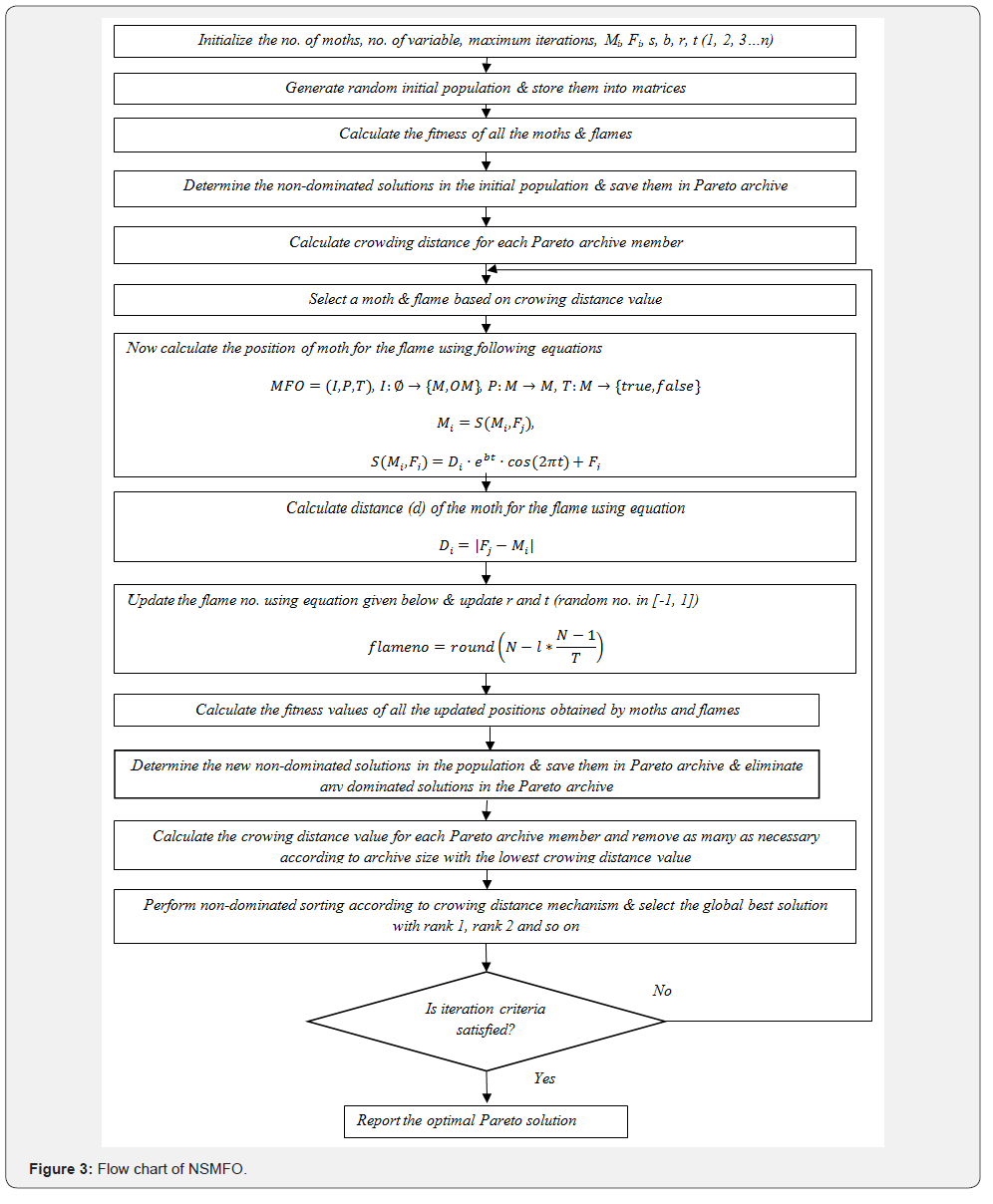
Basic working of NSMFO algorithm is as follows
Stage 1:
a. First of all, initialize the population of moths
b. Randomly generated sets of moths & flames are
represented in matrix for convenience to understand
c. Then fitness of moths & flames is calculated on an
according as objective function
Stage 2:
a. Position of moths in a spiral path is a function of the
position of moths and flames
b. The value of absolute distance is achieved which is
basically a distance between the current best solution to the
final optimal solution
c. Then exact position of moths & flames is achieved which
is a mathematical spiral function of with a product of actual
distance between them and an addition of the position of
flame.

Where, J is a function that generates a random population of
moths and their fitness values. Q is a function, moves the moths
around unknown search space and G comes true when termination
criterion fulfilled else false comes.
Step 3
a. Termination counter in integrated to limit/forcefully
stop the search in uncertain search space (max. iteration
counter to forcefully converge the search to optimal one)
b. Size of the flame matrix is continuously reduced over the
course of iteration due to directed search to find global best
solution (Quick sorting is used to provide directional search)
c. Continuously position of the moths and flames is updated
via a spiral function equation for each iteration
Step 4
a. Likewise, multi-objective optimization the NSMFO
algorithm is made to capable to store the pareto optimal
solutions in a collection set and make it as flexible to change
solution over the course of iteration
b. Solution is assigned a rank according to their ability as
if a solution is not dominated by other solution is assigned
rank1, dominated by only solution assigned rank 2 and so on &
if collection set is full over predefined size then some solutions
that are dominated in nature are directed to be out from the
collection set according to the crowding distance mechanism.
This collection set is similar to the term achieve used in MOSOS
and NSGA-II. It is a repository to store the best non-dominated
solutions obtained so far. The search mechanism in NSMFO is
very similar to that is MFO, in which solutions are improved using
moths. Due to the existence of multiple best solutions, however,
the best moth should be chosen from the collection set.
In order to select solutions from the archive to establish tunnels
between solutions, we employ a leader selection mechanism. In
this approach, the crowding distance between each solution in
the archive is first selection and the number of solutions in the
neighbourhood is counted as the measure of coverage or diversity.
We require the NSMFO to select solutions from the less populated
regions of the archive using the following equation to improve the
distribution of solutions in the archive across all objectives.
This subsection proposes multi-objective version of the MFO
algorithm called NSMFO. The non-dominated sorting has been
of the most popular and efficient techniques in the literature of
multi-objective optimization. As its name implies, non-dominated
sorting sort Pareto optimal solutions based on the domination
level and give them a rank. This means that the solutions that
are not dominated by any solutions is assigned with rank 1, the
solutions that are dominated by only one solution are assigned
rank 2, the solutions that are dominated by only two solutions are
assigned rank 3, and so on. Afterwards, solutions are chosen to
improve the quality of the population base on their rank. The better
rank, the higher probability to be chosen. The main drawback of
non-dominated sorting is its computational cost, which has been
resolved in NSGA-II.
The success of the NSGA-II algorithm is an evidence of the
merits of non-dominated sorting in the field of multi-objective
optimization. This motivated our attempts to employ this
outstanding operator to design another multi-objective version
of the MFO algorithm. In the NSMFO algorithm, solutions are
updated with the same equations presented in equation (12) In
every iteration, however, the solutions to have optimal position of
moths and flames are chosen using the following equation:

Where c is a constant and should be greater than 1 and i Rank
is the rank number of solutions after doing the non-dominated
sorting.
This mechanism allows better solutions to contribute in
improving the solutions in the population. It should be noted that
non-dominated sorting gives a probability to dominated solutions
to be selected as well, which improves the exploration of the
NSMFO algorithm.
Constraint handling approach
With the extended literature survey, we find that the
population-based algorithms are the common way to solve the
multi-objective problems as they are more commonly provides
the global solution and capable of handling both continuous and
combinational optimization problem with a very high coverage and
convergence. Multi-objective problems are subjected to various
types of constraints like linear, non-linear, equality, inequality
etc. So, with these problems embedded it is very difficult to find
simple and good strategy to achieve considerable solutions in the
acceptable criterion. So in this paper NSMFO algorithm uses a
very simple approach to get feasible solutions. In this mechanism,
after generating number of solutions at each generation, all the
desirable constraint checked and then some solution that fulfils the criterion of acceptable solution are selected and collected
them in achieve. Afterward non-dominated solutions added
in archive as we find more suitable solution to get acceptable
solution. So as if achieve is full then less dominated solutions are
removed. Finally, according to crowing distance mechanism all
these solutions (more suitable position of moths and flames) from
archive is selected to get desired solution (figure 3).
Results Analysis on Test Functions
For determine the performance of proposed NSMFO algorithm
is applied to:
a. A set of unconstraint and constraint standard multiobjective
test functions
b. Tested on well-known engineering design problems
c. Non-linear, highly complex practical application known
as formulation of economic constrained emission dispatch
(ECED) with stochastic integration of wind power (WP) in the
next section
NSMFO algorithm is tested on seventeen different multiobjective
case studies, including eight unconstrained test
functions, five constrained test functions, and four real world
engineering design problem, later algorithm is applied to the main
application economic constrained emission dispatch with wind
power (ECEDWP). These can be classified into four groups given
below:
a. Standard multi-objective unconstrained test functions
(KUR, FON, ZDT1, ZDT2, ZDT3, ZDT4, SCHN1, and SCHN2)
b. Standard multi-objective constrained test functions
(TNK, OSY, BNH, SRN, and CONST)
c. Real world engineering multi-objective design problem
(Four bar truss design, welded beam design, speed reducer
and disk brake design problem)
d. Modelling of ECEDWP problem
Mathematical representation of these standard test functions
are given in Appendix
1. (Multi-objective unconstrained test functions),
2. (Multi-objective constrained test functions),
3. (Engineering multi-objective design problem)
with distinct characteristics like non-linear, non-convex,
discrete pareto fronts and convex etc. are selected to measure the
performance of proposed NSMFO algorithm.
To deal with real world engineering design problem is really
a typical task with unknown search space, in this article we
include four different engineering problems are considered and
performance is compared with various well-known algorithms
like MOWCA, NSGA-II, MOPSO, PAES and μ -GA multi-objective
algorithms. Each algorithm is separately runs fifteen times and
numeric results are listed in tables below. To measure the quality
of obtained results we match their coverage of obtained true pares
to front with respect to their original or true pareto fronts.
For numeric as well as qualitative performance of purposed
NSMFO algorithm on various case studies we consider Generational
Distance (GD) given by Veldhuizen in 1998 [39] for measuring the
deviation of the distance between true pareto front and obtained
pareto front, Diversity matric (Δ) also known as matrix of spread
to measure the uniformly distribution of non-dominated solution
given by Deb [24] and Metric of spacing (S) to represent the
distribution of non-dominated distribution of obtained solutions
by purposed algorithm given by Schott [40].
The mathematical representation of this performance
indicating metric are as follows:

Where di shows the Euclidean distance (calculated in the
objective space) between the ith Pareto optimal solution achieved
and the nearest true Pareto optimal solution in the reference set,
nPFs is the total number of achieved Pareto optimal solutions.

Where, , l m d d are Euclidean distances between extreme
solutions in true pared to front and obtained pared to front. i d
Shows the Euclidean distance between each point in true Pareto
front and obtained Pareto front. nPFs and ‘d’ are the total number
of achieved Pareto optimal solutions and averaged distance of all
solutions

Where “d” is the average of all i d , nPFs is the total number of
achieved Pareto optimal solutions, and
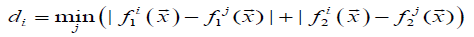
for all i,j=1,2,…,n. Smallest value of “S” metric gives the global
best non-dominated solutions are uniformly distributed, thus
if numeric value of i d and d are same then value of “S” metric is
equal to zero.
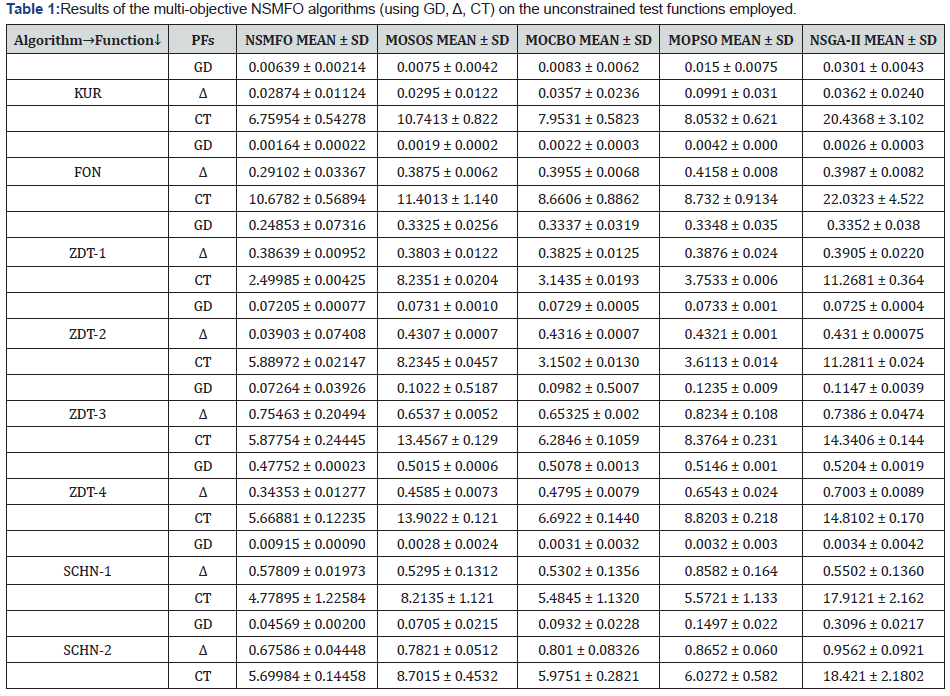
Results on unconstrained test problems
Like as above mentioned, the first set of test problems
consist of unconstrained standard test functions. All the standard
unconstrained test functions mathematical formulation is shown
in Appendix A. Later, the numeric results are represented in Table
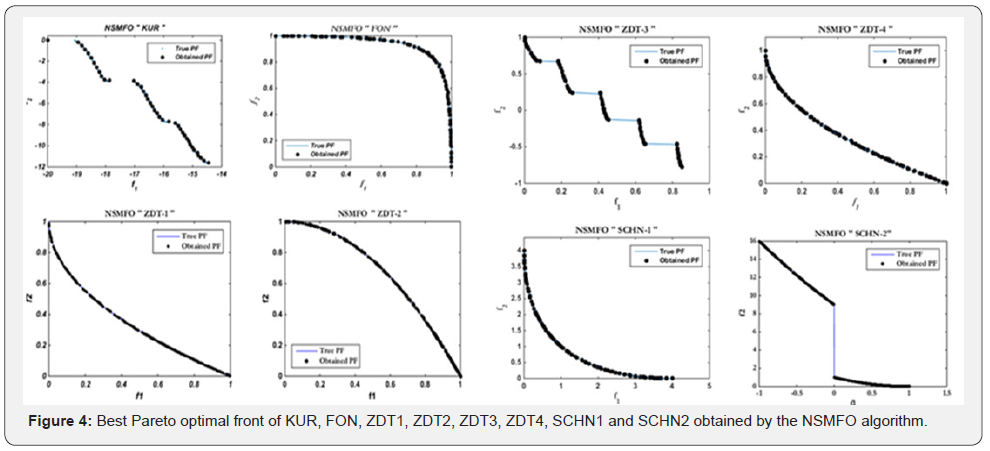
1 and best optimal Pareto front is shown in Figure4.
All the statistical results are shown Table 1 suggests that
the NSMFO algorithm effectively outperforms with most of the
unconstraint test functions compare to the MOSOS, MOCBO,
MOPSO and NSGA-II algorithm. The effectiveness of proposed
non-dominated version of MFO (NSMFO) can be seen in the
Table 1, represents a greater robustness and accuracy of NSMFO
algorithm in terms of mean and standard deviation with the help of GD, diversity matrix along with computational time. However,
proposed NSMFO algorithm shows very competitive results in
comparison with the MOPSO, MOCBO and MOSOS algorithms and
in some cases these algorithms performs better than proposed
one. Pareto front obtained by proposed NSMFO algorithm shows
almost complete coverage with respect to true pareto front
(Figure4).
Results on constrained test problems
The next set of standard test functions consisting of
constrained functions. For constrained test function it should
be necessary that NSMFO algorithm has a capability of handling
constraints so algorithm is equipped with a death penalty function
to search agents that violate any of the constraints at any level
[41]. For comparing the results of different algorithms, we have
utilized GD and Δ metrics (Table 2).
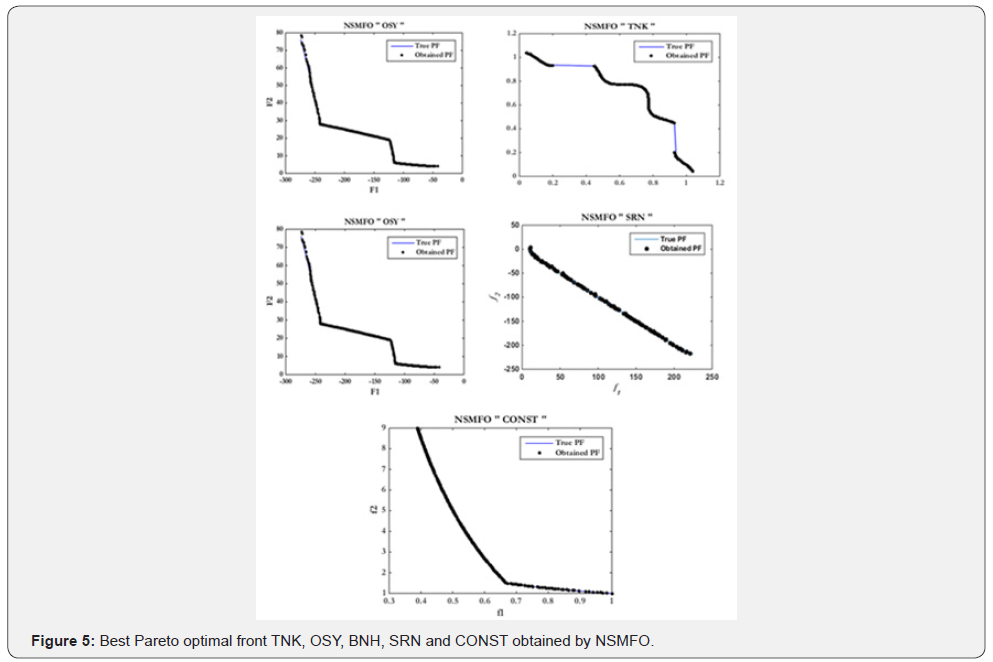
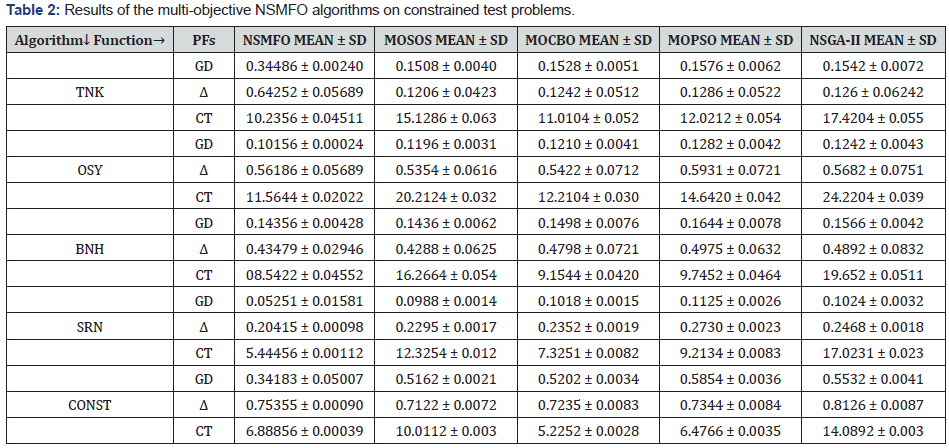
Table 2 suggests that the NSMFO algorithm
comparatively
performs better than other four algorithms for most of the
standard constrained test functions employed. The best Pareto
optimal fronts in Figure 5 also helps in proving since all the Pareto
optimal solutions exactly follow the true Pareto fronts obtained
from by NSMFO algorithm.
CONST function consists of concave front with linear front,
OSY is similar to CONST but consists of many linear regions with
different slops while TNK almost similar to wave shaped. These
also suggest that NSMFO algorithm has a capability to solve various
type of constraint problem. All the constraint test functions are
mathematically given in Appendix B.
Results on constrained engineering design problems:
The third set of test functions is the most complicated one and
consists of four real engineering design problems. Mathematical
model of all the four engineering design problem are given in
Appendix C. Same as before both GD and diversity matrix is
employed to measure the performance of NSMFO algorithm
with respect to other algorithms to solve them, numeric results
are given in Table 3 and Figure 6 shows the best optimal front
obtained by NSMFO algorithm.

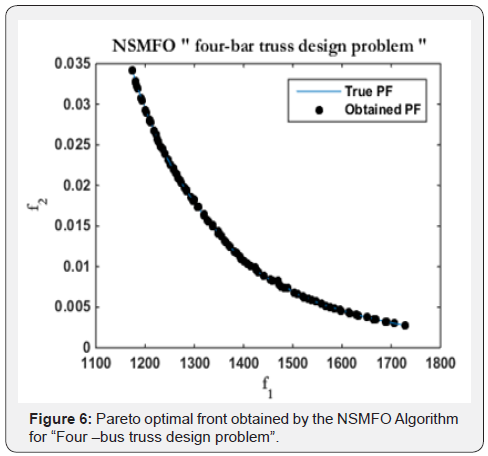
Four-bar truss design problem: The statistical results of
four bar truss design problem [42] in given in Table 3 and best
optimal front is given in Figure 6 It consists of two minimization
objectives displacement and volume with four design control
variable mathematically given in Appendix C (Figure 7).
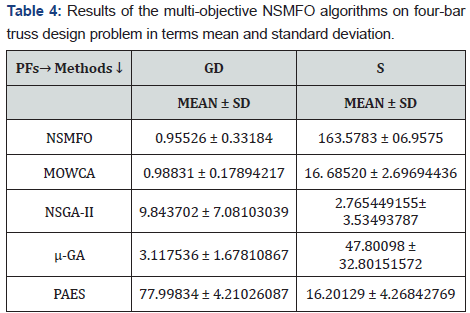
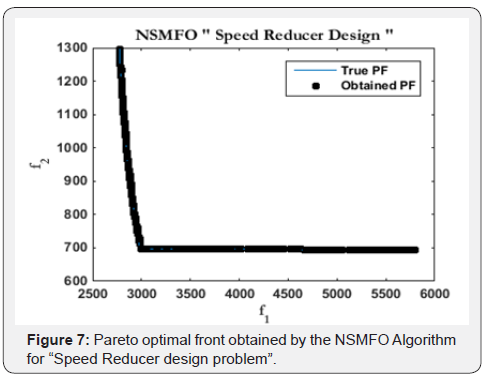
Speed-reducer design problem: The statistical results of
speed reducer design problem [43] is given in Table 4 and best
optimal front is given in Figure 7 It is a well-known mechanical
design problem consists of two minimization objectives stress and
weight with seven design control variable mathematically given in
Appendix C.
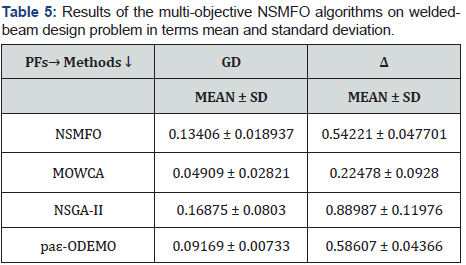
Welded-beam design problem: The statistical results of
welded beam design problem [44] is given in Table 5 and best
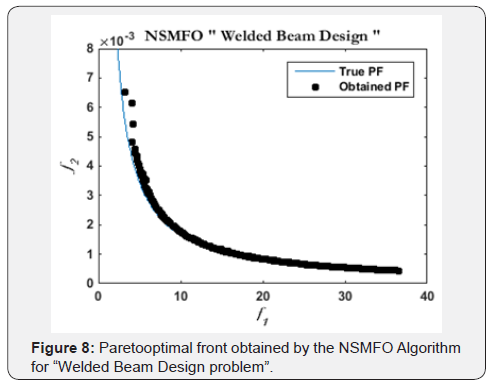
optimal front is given in Figure 8. It is a well-known mechanical
design problem consists of two minimization objectives
fabrication cost and deflection of beam with four design control
variable mathematically given in Appendix C.
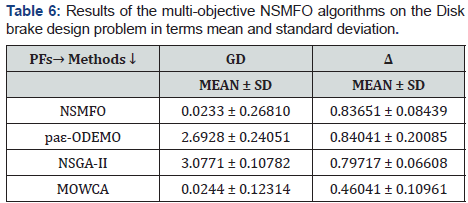
Disk brake design problem: The statistical results of welded
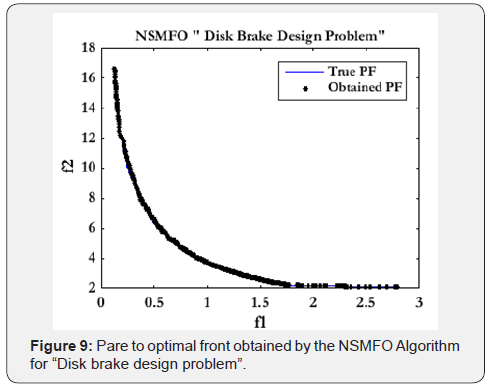
beam design problem [44] is given in Table 6 and best optimal
front is given in Figure 9. It is a well-known mechanical design
problem consists of two minimization objectives stopping time
and mass of brake of a disk brake with four design control variable
mathematically given in Appendix C.
Due to high complexity of engineering design problem it
is really hard to gain results alike true pareto front but we can
clearly see that optimal pareto obtained by NSMFO algorithm is
covers almost whole solutions that are the actual/true solutions
of an engineering design problem. From all above testedfunction
we can conclude that problem either it consists of constraints
or unconstraint problem NSMFO algorithm shows its capability
to solve any kind of linear, non-linear and complex real world
problem. So in the next section we attached a highly non-linear
complex real problem to show its effectiveness regarding the real
world complex application with many objectives.
Formulation of economic constrained emission dispatch (ECED) with integration of wind power (WP)
Mathematical formulation of wind power: In case of
wind power generation the Output power of wind generator
is calculated with the help of a stochastic variable wind speed
υ (meter/seconds). Wind speed is a variable function so there
probability distribution plays a very important role. Wind
speed mathematically formulated as two-parametric Weibull
distribution function, probability density function (PDF) and
cumulative distribution function (CDF) as follows:
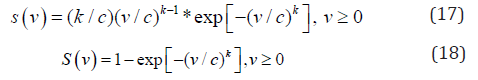
Where, S(v) and s(v) are CDF and PDF respectively. Shape
factor and scale factor are k and c respectively.
The wind speed and output wind power are related as:
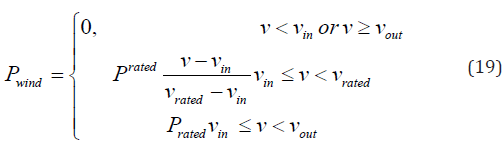
Where, rated v and rated P are the rated speed of wind and rated
power output. out v and in v are cut-out and cut-in speed of wind
respectively. The CDF of wind P in the boundary of [0, rated P ] on an
accordance with the speed range of wind can be formulated as:

Above equation is very meaningful to calculate the ECED
problems with speculative wind power with variable speed.
Modelling of ECEDWP problem: As wind power is
formulated as system constraint, sothe objective function of
economic emission dispatch problem (EEDP) stays on unchanged
as classical EEDP:Fuel cost objective is given by:
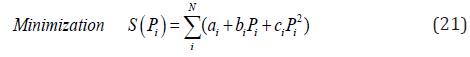
Where, the thermal power generators cost coefficients are
ai,bi,ci for ith generator, Sum of the total fuel cost of the system
and N is the total number of generators.
Total Emission is calculated by:
Minimization E P=

Where αi, βi, γi, δi and ϕi
are emission coefficients with valve
point effect taking into consideration for ith thermal generator.
System constraints: As wind power generation is considered
as system constraint with the summation of stochastic variables
the classical power balance constraint changes to fulfil the
predefined confidence level.
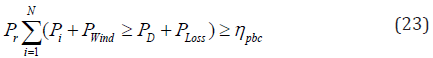
Where, ηpbc is confidence level that a power system must
follow the load demand and so as it is selected nearer to unity
as values lesser than unity represents high operational risk.
Ploss represents system losses can be calculated by B-coefficient
method given below:

So as to change above described power balance constrained
equation into deterministic form can be solved as:
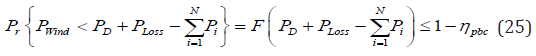
Assume that the wind turbine have same speed and same
direction and combination of Eqs. (25), the power balance
constraint is represented as:
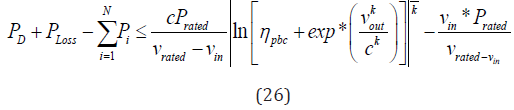
Reserve capacity system constraint: So as to reduce the
impact of stochastic wind power on system, up and down spinning
reserve needs to be maintained [22]. Such reserve constraints
formulated as [15] and [16] respectively:
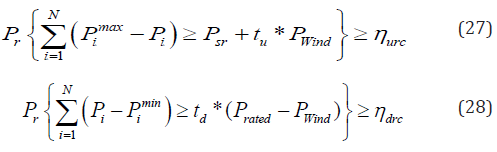
Where, sr Psr represents the reserve demand of conventional
thermal power plant system and it generally keeps the maximum
value of thermal unit, Pimax and Pimin
are maximum and minimum
output level of operational generators of ith unit, ηdrc and ηurc
are predefined down and upper confidence level parameter
respectively, tu and td are the demand coefficients of up and down
spinning reserves
Generational capacity constraint: The real output power is
bounded by each Generators upper and lower bounds given as:
.
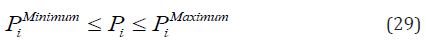
40-Operational Thermal Generating Unit
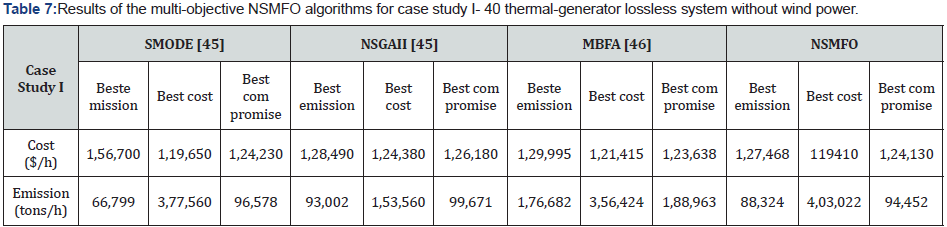
Case study I- 40 thermal-generator lossless system without wind power
In this case forty operational generating unit is consider
without integration of wind power means all the generating
units are coal fired. Input parameters like generators operating
limit, fuel cost coefficients and emission coefficients are given in
Appendix D extracted from [45]. System is considered lossless and
its solution is compared with three well known multi-objective
algorithms like SMODE [45], NSGA-II [45] and MBFA [46] in terms
of various objectives such as best cost, best emission and best
compromise between both objectives. Best compromise solution
is then obtained by the fuzzy based method [47]. Total power
demand for this system is 10500 MW. Results obtained by NSMFO
algorithm is added to Table 7 and best Pareto front obtained by
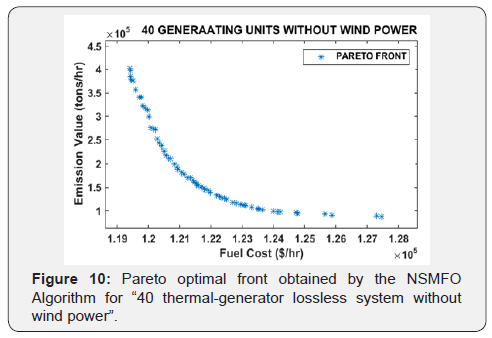
NSMFO algorithm is represented in Figure 10.
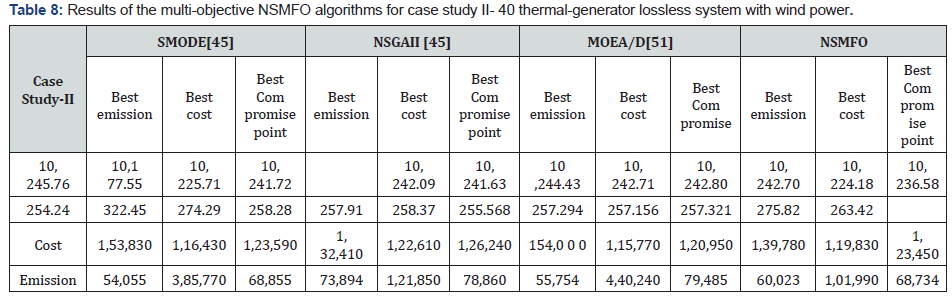
Case study II- 40 thermal-generator lossless system with wind power
All the conditions are remaining same as case study I like
input parameters and power demand. While integrating with
wind power plant, the total rated output power of wind farm is
set to 1000 MW [45,47]. Statistical results obtained by NSMFO
algorithm is reported in Table 8 [51] and best optimal front is
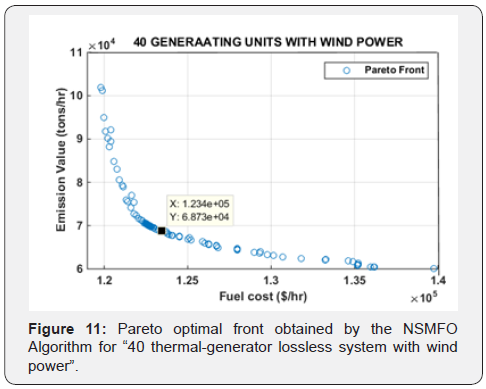
represented in Figure 11.
Result & Discussion
In almost all the cases that we consider in this article where
NSMFO algorithm proves its effectiveness in both respects
quantitative and qualitative. From plots also evident that NSMFO
algorithm follows the exact pareto front similar to the true pareto
front for all constrained, unconstrained and complex engineering
design problem. So as for real world application of economic
emission dispatch problem and its integration with stochastic
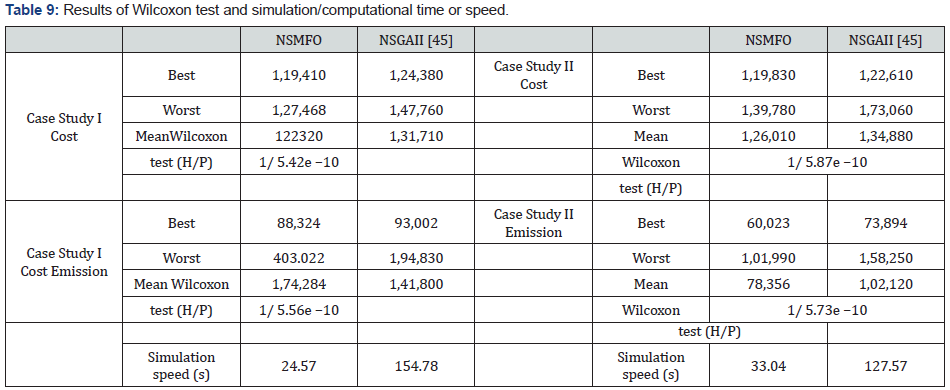
wind power generation [48-51]. So, for this application Wilcoxon
test (statistical test) is performed. In Table 9 the signed rank test is
presented in forth row of each results whereas the calculation time
is represented in third row. For this test null hypothesis cannot be
rejected at 5% level for numeric value ‘0’ while null hypothesis is
rejected at 5% level with the value of ‘1’. Where NSMFO algorithm
performs superior to other algorithms that are considered for
comparative purpose. NSMFO algorithm shows good performance
in both coverage and convergence as main mechanism that
guarantee convergence in MFO and NSMFO are continuously
shrink its virtual limitation in the movement of moths and flames
for their random walk. Both mechanisms emphasize convergence
and exploitation proportional to maximum number of generation
(iteration). Since this complex task might degrade its performance
compare to without limitation or free movement should be a
concern. However, the numerical results express that NSGWO
algorithm has a little effect of slow convergence at all.
NSMFO algorithm has an advantage of high coverage, which
is the result of the selection of position of moth and flame and
archive selection procedure. All the position is updated according
to their fitness value that enable the algorithm to direct the search
space in right direction to find the best solution without trapped
in local solution. Archive selection criteria follow all the rules
of the entrance and exhaust of any value in it for each iteration
and updated when its size full. Solutions of higher fitness in
archive have higher probability to thrown away first to improve
the coverage of the pareto optimal front obtained during the
optimization process.
Conclusion
In this paper the non-dominated MFO multi-objective version
of recently proposed moth flame optimizer (MFO) algorithm is
proposed known as NSMFO algorithm. This paper also utilizes
the transverse orientation strategy for exploration purpose used
in its parent MFO version. NSMFO algorithm is developed with
equipping MFO with crowding distance criterion, an archive
and moth-flame position (accordance to ranking) selection
method based on Pareto optimal dominance nature. The NSMFO
algorithm is first applied on 17 standard test functions (including
eight unconstraint, five constraints and four engineering design
problem) to prove its capability in terms of qualities and quantities
showing numerical as well as convergence and coverage of pareto
optimal front with respect to true pareto front. Then after NSMFO
algorithm is applied to real world complex ECEDWP problem
where algorithm proves its dominance over other well recognized
contemporary algorithms. The numeric results are stored and
represented in performance indices: GD, metric of diversity, metric
of spacing and computational time. The qualitative results are
reported as convergence and coverage in best pareto optimal front
found in 15 independent runs. To check effectiveness of proposed
version of algorithm the results are verified with SMODE, MOSOS,
MOCBO, MOPSO, NSGA-II and other well recognize algorithms in
the field of multi-objective algorithms. We can also conclude from
the standard test functions results that NSMFO algorithm is able
to find Pareto optimal front of any kind of shape. Finally, the result
of complex real world ECEDWP problem validates that NSMFO
algorithm is capable of solving any kind of non-linear and complex
problem with many constraint and unknown search space.
Therefore, we conclude that proposed non-dominated version
of MFO algorithm has various merits among the contemporary
multi-objective algorithms as well as provides an alternative for
solving multi or many objective problems.
For future works, it is suggested to test NSMFO algorithm on
other real world complex problems. Also, it is worth to investigate
and find the best constrained handling technique for this algorithm
(Appendix) [48-50].
For more articles in Open Access Journal of
Engineering Technology please click on:



Comments
Post a Comment