DNS on the Evolution of Vortices in the Upper Boundary Layer in Transition - Juniper Publishers
Juniper Publishers - Open Access Journal of Engineering Technology
Abstract
The ring-like vortices (or hairpin vortices) are
universal vortical structures in late boundary layer transition. They
play a very important role in the boundary layer transition process. In
this paper, the development of ring-like vortices and the mechanism of
sustainability of these vortices in the upper boundary layer are
investigated numerically by direct numerical simulation (DNS). Intense
interaction among ring-like vortices and the other vortical structures
in different vortical packets which generated at different time are
observed. It shows that steamwise counter-rotating cores will generate
new ring-like vortices and the ring-like vortices become more stronger
and raise to the upper boundary layer after mutual interaction and
merging. In the meanwhile, the boundary layer of the late transition
becomes thicker.
Keywords: Evolution;
Transition; Vortical structures; Interaction; Filaments flow;
Parameters; Simulation; Instability; Downstream; Aggregations;
Transitional flowIntroduction
Experimental and numerical results show that when the
ring-like vortex structures (hairpin or Ω-shaped vortices) are formed
[1-5], the late boundary layer transition begins. Almost at each
transitional stage of a boundary layer, these structures are usually
found in larger vortex packages. It has also been found that they are
the dominant mechanism of perturbation in the late stages of
boundary-layer transition.
It is, of course, very important to understand the
formation and evolution of Λ vortex structures (especially the ring-like
vortices) and the evolution of Λ vortex packages which is associated
with the onset of the flow transition. In order to gain a better
understanding of the transition process at the late stage, we used a
high-order DNS to study its mechanisms in a boundary layer [6-11]. In
our previous work [8], we studied the origin and formation of vortex and
ring-like vortex numerically. It is found that the widely recognized
process, the self-deformation Λ of vortex into a ring-like vortex, does
not exist. The so-called hairpin vortex is actually the combination of
separated Λ vortex and ring-like vortex. The Λ vortex in the upstream is
not a general vortex tube. Indeed, it is a pair of open rotation cores
[8,9]. The roots of Λ vortex are formed by special gathering of vortex
filaments. On the other hand, ring-like vortices are formed separately
and independently. The ring-like vortices and the Λ vortex roots are
generated separately by different mechanisms. It is confirmed that the
shear layer near the top edge of the boundary is unstable and it will
produce such ring-like vortex structures [7].
The purpose of this paper is to further study the
mechanism of boundary layer growth during the transition. The evolution
of ring-like vortices and vortical packets is studied in detail. In
Section II, We briefly introduce the case settings and code validation;
in Section III, the vortex structure and its mechanisms from our DNS
observation are specified; in Section IV, the evolution process and
mechanism of ring-like vortex and vortex package are studied. Finally,
we give our conclusions.
Case Setup and Code Validation
Case setup
This paper employs DNS to study the transition
process on a flat plate. The grid system we used is 1920 × 128×241,
representing the number of grids in the direction of the streamwise (x),
the spanwise (y) and the wall normal(z). In the normal direction, the
grid is stretched. In the streamwise and spanwise directions, the grids
are evenlydistributed. At the inlet, the length of the first grid
interval in the normal direction is 0.43 in wall units (y+=0.43). Table 1
lists the flow parameters in our simulation, including Mach number,
Reynolds number etc. Here, in x represents the distance between leading
edge and
inlet, Lx,Ly,Lzin are the lengths of the computational domain in
x − , y − , z − and z − directions, respectively, and is the wall
temperature.
Code validation
The validations by NASA Langley and UTA researchers of our
DNS code can be found in [3-5]. The DNS resultsare well verified
by comparison with theoretical and experimental data and are
consistent with other DNS results [6-9].

By using the Ω visualization method [12], the vortex structures
initialed by the nonlinear evolution of T-S wavesduring the
transition are shown in Figure 1. Reference 8-11 give details of
the evolution. The formation of ring-likevortex chains coincides
with the experimental results [13] and the numerical results of
Rist and his co-authors (Bake et al. [14]).
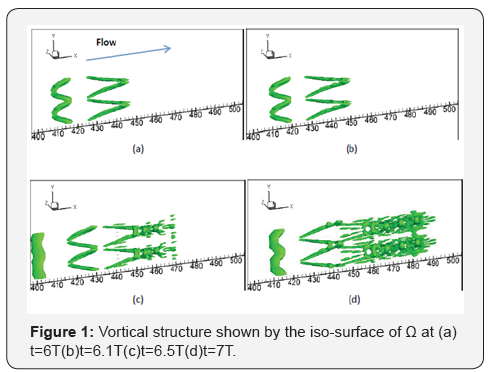
DNS Observations on the Vortical Structures in the Boundary Layer
Figure 1 shows the vortical structure from our numerical
simulation at different time steps are visualized by the is
surfaceof Ω (Ω= 0.5). At t=6.0T, the Λ vortex in Figure 1a is still
open at the tip. However, at t=6.1T, the first ring-likevortex will
soon be generated at the tip of the vortex. After that, more ringlike
vortices are generated above the Λ vortex when it travels to
the downstream (see Figure 1c and 1d).
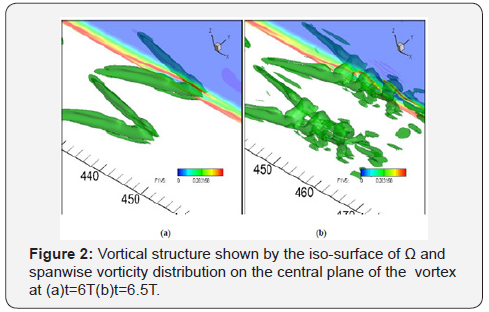
Our previous work [7,8] pointed out that the high shear layer
between the roots of Λ vortex (see Figure 2a) is the mechanism
by which the ring-like vortices are generated. The high shear is
initiated by the input TS waves and formed by rotation effect of
the roots of the vortex, especially the ejection which brings the
low speed fluid up to approach the high-speed fluids and forms
a very strong shear. This very strong shear layer in the middle
of Λ-vortex roots is unstable and will break up (see Figure 2b)
to several pieces. The ring-like vortices above the Λ-vortex are
formed by the breakdown of the shear layer corresponding the
Kelvin-Helmholtz instability
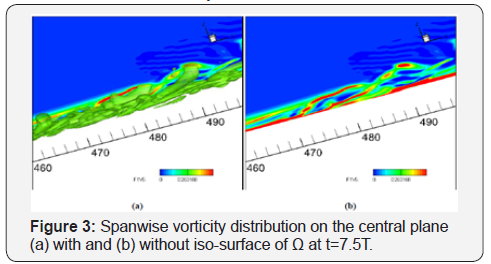
Once the ring-like vortices are formed, the ejecting and
sweeping effect [6,9] becomes more intense as we call the second
ejection and second sweep. Along with the streamwise vortical
structures (such as Λ vortices), low speed zones will be rolled
up successively. On the up-bound of these low speed zones, new
strong velocity shear layers will be formed (See Figure 3). Most
of these velocity shear layers are unstable, and they will also
break down to produce more secondary ring-like vortices. At the
same time, the streamwise vortical structures will cause more
counter-rotating secondary streamwise vortical structures (see
Figure 1d). The energy from the free stream and the spanwise
vorticity from the lower boundary layer will contentiously trigger
or indirectly produce more vortices under the first generated
ring-like vortices [9]. The vortical structure soon becomes very
complicated. Each vortex will eventually form a vertical packet
in the downstream (see Figure 1d and Figure 4). The vertical
packets grow and become wide enough to interact with each
other (see Figure 4b). The neighboring vortical packets in the
direction of spanwise inevitably converge together.
DNS Observations on the Growth of Ring-like Vortices
Figure 5 shows the vortical structure in the boundary layer
at t=10T. The ring-like vortices at different levels are continually
generated. They dominate the development of the boundary
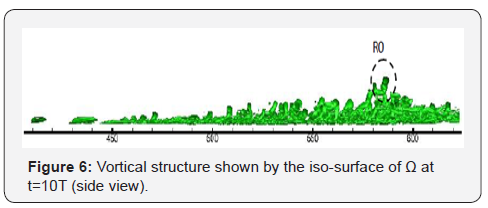
layer, especially the upper boundary layer (see Figure 6).

As we know, the tilted ring-like vortices will be raised up by
self-induction. In such process, however, the ring-like vortices
would be weakened due to dissipation in the upper boundary.
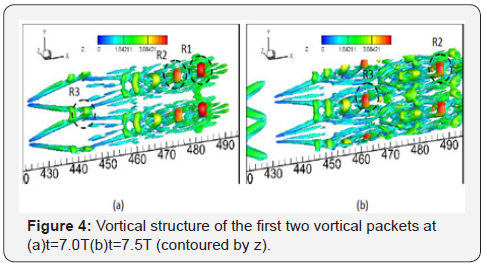
Figure 7a shows the change of height of the first and second ringlike
vortices in Figure 4 (marked as R1 and R2) when they are
traveling to the downstream. These two vortices stop raising up
in the downstream. Accordingly, the spanwise vorticity at the
tops of them keeps decreasing (see Figure 4b). These ring-like
vortices will be dissipated eventually. Thus, there must exist
other mechanisms for the sustenance and growth of ring-like
vortices at the upper boundary layer (see Figure 5). In order to
investigate the mechanisms, evolution of the highest ring-like
vortex, marked as R0, in Figure 5 and 6 at t=10T is tracked.
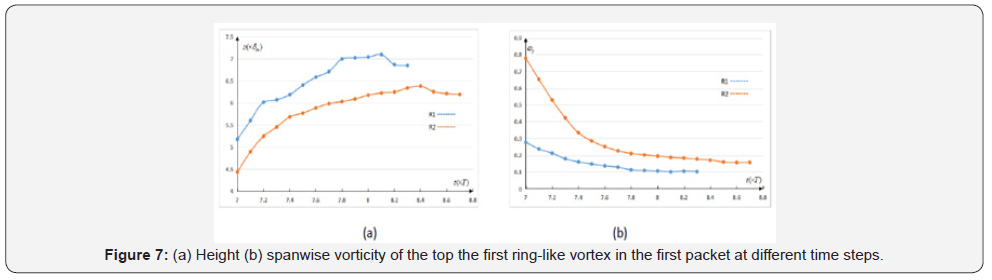
Figure 8 shows the evolution of the vortex R0 in Figure 5
at different time steps. Since the ring-like vortices travel faster
than the spanwise vortical structures (such as Λ-vortices) in
the lower boundary layer, the vortical packet in the upstream
will catch up with the ones in the downstream (see Figure 4b).
The vortex R3 in the second packet starts to interact with a new
generated ring-like vortex (R4 in Figure 8b) in the first packet
at t=8.5T. Eventually, these two ring-like vortex merges together
and become ring-like vortex R0 in Figure 5.
Figure 9 gives the spanwise distribution on the central
streamwise plane in the process of forming the large ring-like
vortex R0. The tops of the vortex R3 and R4 are circled. It can
be seen clearly that the intensity of the ring-like vortex R3 is
reduced a lot before it catches the first vortical packet. However,
it will be strengthened after entering into the first vortical
packet, especially when the interaction happens with R4 - a new
generated ring-like vortex in the downstream. The merge of
these ring-like vortices creates a larger and much stronger ringlike
vortex-R0 (Figure 9c).
Figure 10 shows the vortical structure in the downstream of
the vortex R3 and the distribution of spanwise vorticity on the
central plane. It shows that the newly generated ring-like vortex
R4 at t=8.55T is generated at the upper bound of a shear layer
by the instability of this shear-layer (K-H instability). The shear
layer is created by the up-wash effect of the counter-rotating
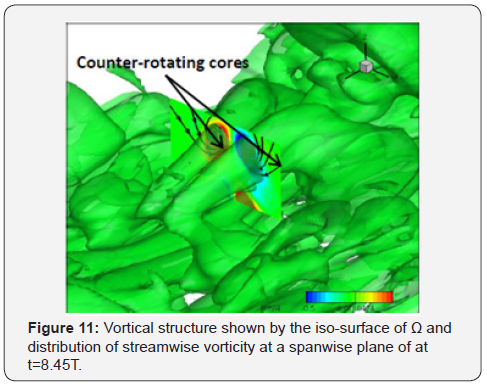
cores (see Figure 10 and 11). This kind of counter-rotating cores
are a common vortical structure in the transitional flow (see
Figure 4b, 8d and10a). They are not vortex tubes but still the
aggregations of vortical filaments which are similar to Λ-vortices
[8]. Strong shear layers are continually formed between these counter-rotating cores and new generations of ring-like vortices
will happen at the upper bounds due to K-H instability (see
Figure 10). The existence of streamwise counter-rotating cores
and the shear layers is one of the mechanisms for generating and
sustaining ring-like vortices in the upper boundary layer in the
transitional flow.
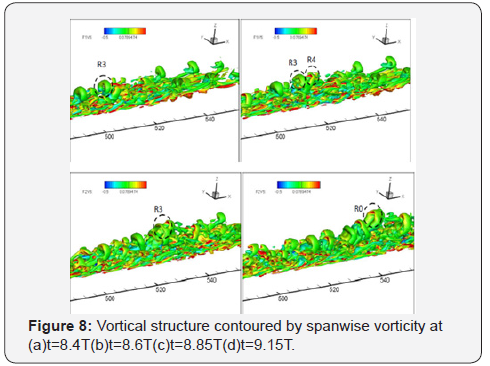
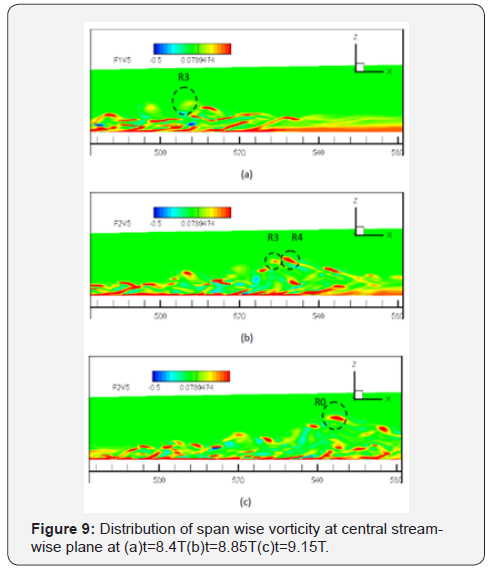
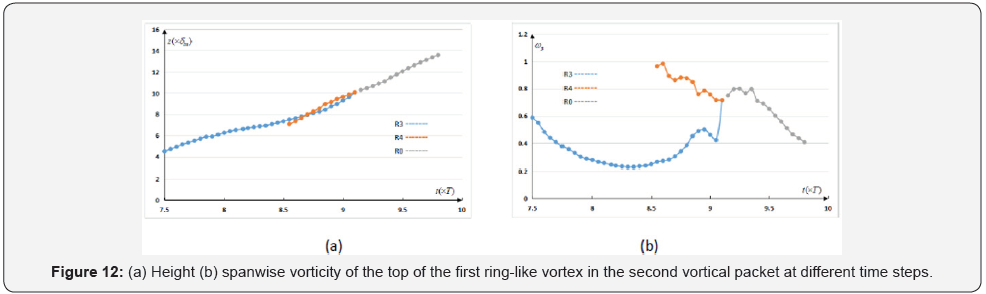
Figure 12a gives the heights of the vortex R3 from 7.5T to
9.7T. It shows that this ring-like vortex keeps rising. The height
of this ring-like vortex is lower than the vortices R1 and R2 in
the first vortical packet at t=7.5T (also see Figure 4). However,
it reaches the height of 13.3δin which is twice as the maximum
height of R1 has ever reached. It must be pointed out that, the
increase of the height of R3 seems linearly, even after it caught
the first vortical packet. There’s no jump on the height after the
second vortical packet mixed with the first packet. When two
vortical packets meet together, the second vortical packet is not
simply pushed up. Complicated interaction among vortices and
other vortical structures will happen.

In Figure 12b, the spanwise vorticity at the top of the ringlike
vortex R3 and R4 is provided. It shows that the ring-like
vortex R3 is first reduced before it catches the first vortical
packet. Then, the intensity of its top become increasing and
oscillating. The vorticity increases and reaches a peak when R3
merges with R4 (become R0) at about t=9.1T. Of course, when
the new generated ring-like vortex R0 keeps arising, it will be
reduced again (see Figure 12b).
During the evolution of vortical structures in the downstream,
more and more different vortical packets are mixed, some of the
ring-like vortices will continually be strengthened by mutually
interaction and merging. In the meanwhile, more secondary
ring-like vortices and other vortical structures will be created.
The boundary layer is thickened gradually during this process. At
last, the typical forest of vortical structure will be formed in the
boundary layer (see Figure 5). The interaction between vortical
packets are very complicated and require further studied in
detail.
Conclusion
In this paper, the study on the development of ring-like
vortices in the transitional flow by DNS (direct numerical
simulation) is given. This includes the mechanisms of the
formation of large ring-like vortices in the upper boundary layer, the mutual interaction among ring-like vortical structures
and the increase of boundary layer thickness. It is found that
the streamwise counter-rotating cores played a very important
role on generating new ring-like vortices in the upper boundary
layer. The ring-like vortical structures generated in different
time and different packets also interacts intensely. Once the
vortical packets meet together, the ring-like vortices will interact
and merge with each other. The strengthened ring-like vortical
structures will move towards a higher position and become
stronger. The boundary layer thus becomes thicker gradually
during the process.
Acknowledgment
The authors are grateful to Texas Advanced Computing
Center (TACC) for providing computation hours. This work was
partially supported by Science and Technology Commission of
Shanghai Municipality (Grant No. 13DZ2260900). This work is
accomplished by using Code DNSUTA which was released by Dr.
Chaoqun Liu at University of Texas at Arlington in 2009.
For more articles in Open Access Journal of
Engineering Technology please click on:




Comments
Post a Comment